Cho hàm số y = x 3 - 3 x 2 + 3 m x + m - 1 . Biết rằng hình phẳng giới hạn bởi đồ thị hàm số và trục Ox có diện tích phần nằm phía trên trục Ox và phần nằm phía dưới trục Ox bằng nhau. Giá trị của m là
A. 2/3.
B. 4/5.
C. 3/4.
D. 3/5.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Ta có: ![]() ;
; ![]() .
.
![]() ;
;
hàm số có hai điểm cực trị ![]()
![]() .
.
Mặt khác ![]() .
.
![]()
![]()
![]() .
.
Hàm số bậc ba có đồ thị nhận điểm uốn làm tâm đối xứng. Do đó:
m cần tìm thoả và điểm uốn nằm trên trục hoành
=> m < 1 và ![]()
![]() .
.

Đáp án D
Phương trình hoành độ giao điểm của đồ thị f ( x ) và Ox: a x 4 + b x 2 + c = 0 .
Để phương trình có bốn nghiệm
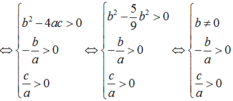
Gọi x 1 , x 2 , x 3 , x 4 lần lượt là bốn nghiệm của phương trình a x 4 + b x 2 + c = 0 và x 1 < x 2 < x 3 < x 4 . Không mất tính tổng quát, giả sử a > 0 .
Khi đó
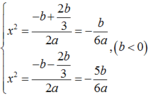
Suy ra x 1 = - - 5 b 6 a ; x 2 = - - b 6 a ; x 3 = - b 6 a ; x 4 = - b 6 a .
Do đồ thị hàm số f ( x ) nhận trục tung làm trục đối xứng nên ta có:
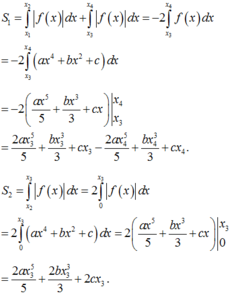
Suy ra
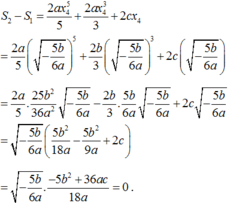
Vậy S 1 = S 2 hay S 1 S 2 = 1 .

Đáp án D
Phương trình hoành độ giao điểm của đồ thị f(x) và Ox: a x 4 + b x 2 + c = 0 .
Để phương trình có bốn nghiệm
⇔ b 2 − 4 a c > 0 − b a > 0 c a > 0 ⇔ b 2 − 5 9 b 2 > 0 − b a > 0 c a > 0 ⇔ b ≠ 0 − b a > 0 c a > 0
Gọi x 1 , x 2 , x 3 , x 4 lần lượt là bốn nghiệm của phương trình a x 4 + b x 2 + c = 0 và x 1 < x 2 < x 3 < x 4 . Không mất tính tổng quát, giả sử a>0.
Khi đó x 2 = − b + 2 b 3 2 a = − b 6 a x 2 = − b − 2 b 3 2 a = − 5 b 6 a , b < 0 .
Suy ra
x 1 = − − 5 b 6 a ; x 2 = − − b 6 a ; x 3 = − b 6 a ; x 4 = − 5 b 6 a
Do đồ thị hàm số f(x) nhận trục tung làm trục đối xứng nên ta có:
S 1 = ∫ x 1 x 2 f x d x + ∫ x 3 x 4 f x d x = − 2 ∫ x 3 x 4 f x d x = − 2 ∫ x 3 x 4 a x 4 + b x 2 + c d x
= − 2 a x 5 5 + b x 3 3 + c x x 4 x 3 = 2 a x 3 5 5 + b x 3 3 3 + c x 3 − 2 a x 4 5 5 + b x 4 3 3 + c x 4 .
S 2 = ∫ x 2 x 3 f x d x = 2 ∫ 0 x 3 f x d x = 2 ∫ 0 x 3 a x 4 + b x 2 + c d x = 2 a x 5 5 + b x 3 3 + c x x 3 0
= 2 a x 3 5 5 + 2 b x 3 3 3 + 2 c x 3 .
Suy ra
S 2 − S 1 = 2 a x 4 5 5 + 2 a x 4 3 3 + 2 c x 4 = 2 a 5 − 5 b 6 a 5 + 2 b 3 − 5 b 6 a 3 + 2 c − 5 b 6 a
= 2 a 5 . 25 b 2 36 a 2 − 5 b 6 a − 2 b 3 . 5 b 6 a − 5 b 6 a + 2 c − 5 b 6 a = − 5 b 6 a 5 b 2 18 a − 5 b 2 9 a + 2 c
= − 5 b 6 a . − 5 b 2 + 36 a c 18 a = 0
Vậy S 1 = S 2 hay S 1 S 2 = 1 .

Câu 2: Đáp án B.
Phương pháp
Hình phẳng được giới hạn bởi hàm số y = f x , trục hoành và các đường thẳng x = a , x = b có diện tích được tính bới công thức:
S = ∫ a b f x d x
Cách giải
Áp dụng công thức tính diện tích hình phẳng ta được:
S = ∫ 1 3 f x d x
Ta có: y ' = 3 x 2 - 6 x + 3 m ; y ' = 0 ⇔ x 2 - 2 x + m = 0
∆’=1-m;
Để có diện tích phần trên và phần dưới thì hàm số phải có hai điểm cực trị →∆’>0→m<1. Mặt khác y”=6x-6.
y”=0→x=1→y=4m-3.
Hàm số bậc ba có đồ thị nhận điểm uốn là trục đối xứng. Do đó, để diện tích hai phần bằng nhau thì điểm uốn phải nằm trên trục hoành.
Vậy 4m=3→m=3/4 .
Đáp án C