Cho tứ diện ABCD có AC = 3a, BD = 4a. Gọi M, N lần lượt là trung điểm của AD và BC. Biết AC vuông góc với BD. Tính MN
A. M N = a 5 2
B. M N = 5 a 2
C. M N = a 7 2
D. M N = 7 a 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

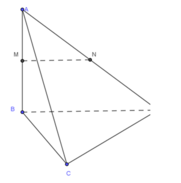
Khối chóp C.BDNM có CB là đường cao nên có thể tích ![]() trong đó
trong đó
+ BC = 2a
+ Tứ giác BDNM là hình thang vuông tại B, M do MN là đường trung bình của tam giác ABD nên
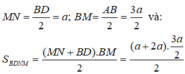
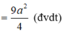
Thể tích của khối chóp C.BDNM là:
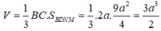

Đáp án C
V C . B M N D V C . A B D = S B M N D S A B C = 3 4 ⇒ V C . B M N C = 3 4 V A B C D = 3 4 . 1 6 . B A . B C . B D = 3 2 a 3
Phương pháp
+) Gọi P là trung điểm của AB. Chứng minh tam giác MNP vuông tại P.
+) Áp dụng định lý Pytago trong tam giác vuông MNP tính MN.
Cách giải