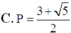
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án B
Ta có log 16 x + y = log 9 x = log 12 y = t ⇔ x = 9 t y = 12 t và
Suy ra 9 t + 12 t = 16 t
⇔ 3 t 2 + 3 t .4 t − 4 t 2 = 0 ⇔ 3 4 t 2 + 3 4 t − 1 = 0
Vậy x y = 9 t 12 t = 3 4 t
⇒ P = 3 4 t 2 + 3 4 t + 1 = 1 + 1 = 2
Đáp án B
log 16 x + y = log 9 x = log 12 y = t ⇒ 16 t = x + y 9 t = x 12 t = y ⇒ x y = 9 t 12 t = 3 4 t 16 t 12 t = 4 3 t = x y + 1
⇒ x y = 3 4 t = 1 x y + 1 ⇔ x y 2 + x y = 1 = P − 1 ⇔ P = 2.
Đáp án C
Đặt
log 9 x = log 12 y = log 16 x + y = t ⇒ x = 9 t y = 12 t x + y = 16 t ⇒ 9 t + 12 t = 16 t
⇔ 3 t 2 + 3 t .4 t − 4 t 2 = 0 *
Chia cả hai vế của phương trình (*) cho 4 t 2 ta được:
3 t 4 t 2 + 3 t 4 t − 1 = 0 ⇔ 3 t 4 t = 5 − 1 2 3 t 4 t = − 5 − 1 2 L ⇒ x y = 3 t 4 t = 5 − 1 2
Ta có:
S = log 4 x 1 + 5 y + log 8 x 1 + 5 y + log 16 x 1 + 5 y 3 + ... + log 2 2018 x 1 + 5 y 2017
= log 2 2 x 1 + 5 y + log 2 3 x 1 + 5 y 1 2 + log 2 4 x 1 + 5 y 1 3 + ... + log 2 2018 x 1 + 5 y 1 2017
= 1 1.2 log 2 x 1 + 5 y + 1 2.3 log 2 x 1 + 5 y + 1 3.4 log 2 x 1 + 5 y + ... + 1 2017.2018 log 2 x 1 + 5 y
= ( 1 − 1 2 + 1 2 − 1 3 + 1 3 − 1 4 + ... + 1 2017 − 1 2018 ) . log 2 x 1 + 5 y
= 1 − 1 2018 . log 2 x 1 + 5 y = 2017 2018 . log 2 5 − 1 5 + 1 2 = 2017 2018
Thay y = 4 x vào biểu thức P và biến đổi ta thu được
P = - 9 log 2 2 + 27 log 2 x - 27 .
Do y ≥ 1 nên x ≤ 4 . Suy ra 1 2 ≤ x ≤ 4 . Đặt t = log 2 x , khi đó - 1 ≤ t ≤ 2 .
Xét hàm số f(t0 = - 9 t 2 + 27t - 27; t ∈ - 1 ; 2
Ta có f ' (t) = -18t + 27; f ' (t) = 0 ⇔ t = 3 2
f (-1) = -63; f (2) = -9; f 3 2 = 27 4
Vậy
m a x P = - 27 4 ⇔ x = 2 2 ; y = 2
Đáp án A
Đáp án B
Đặt log 9 x = log 12 y = log 16 x + y = t ⇔ x = 9 t y = 12 t và x + y = 16 t
Suy ra 9 t + 12 t = 16 t ⇔ 3 t 2 + 3 t .4 t − 4 t 2 = 0 ⇔ 3 4 t 2 + 3 4 t − 1 = 0 ⇔ 3 4 t = − 1 + 5 2
Vậy x y = 9 t 12 t = 3 4 t = − 1 + 5 2 = − a + b 2 ⇔ a = 1 b = 5 ⇒ P = a b = 5
Theo bài ra ta có:
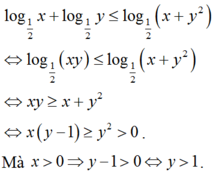
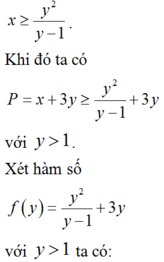
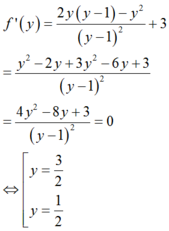
BBT:
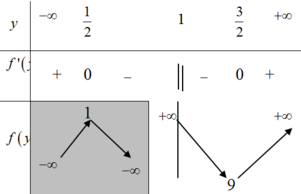
Từ BBT ta thấy
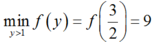
Vậy P ≥ 9 hay P m i n = 9 .
Chọn C.
Đáp án B
Đặt