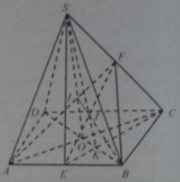
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của AB, SC. Gọi I, K lần lượt là giao điểm của các đường thẳng AN, MN với mặt phẳng (SBD). Tỉ số B I B K bằng
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Chọn A
Do B, I, K thẳng hàng, trong DABN kẻ MF//BI, FÎAN
=>F là trung điểm của AI. Suy ra BI/BK =4/3

À, tưởng dài mà thực ra cũng dễ thôi, vì toàn điểm đặc biệt cả.
Gọi O là tâm đáy \(\Rightarrow I\) là giao AN và SO
\(\Rightarrow I\) là trọng tâm SAC \(\Rightarrow\dfrac{SI}{SO}=\dfrac{2}{3}\)
Gọi E là giao điểm CM và BD, trong mp (SCM) nối MN cắt SE tại J
E là trọng tâm ABC \(\Rightarrow\dfrac{BE}{BO}=\dfrac{2}{3}\)
Menelaus tam giác BOI:
\(\dfrac{BE}{EO}.\dfrac{OS}{SI}.\dfrac{IJ}{JB}=1\Rightarrow2.\dfrac{3}{2}.\dfrac{IJ}{JB}=1\Rightarrow JB=3IJ\)
\(\Rightarrow IB-IJ=3IJ\Rightarrow\dfrac{IB}{IJ}=4\)

a: Gọi O là giao điểm của AC và BD
Chọn mp(SAC) có chứa AN
\(O\in AC\subset\left(SAC\right);O\in BD\subset\left(SBD\right)\)
Do đó: \(O\in\left(SAC\right)\cap\left(SBD\right)\)
mà \(S\in\left(SAC\right)\cap\left(SBD\right)\)
nên \(\left(SAC\right)\cap\left(SBD\right)=SO\)
Gọi I là giao điểm của SO với AN
=>I là giao điểm của AN với mp(SBD)
Chọn mp(AMN) có chứa MN
\(B\in AM\subset\left(AMN\right)\)
\(B\in BD\subset\left(SBD\right)\)
Do đó: \(B\in\left(AMN\right)\cap\left(SBD\right)\)
mà \(I\in\left(AMN\right)\cap\left(SBD\right)\)
nên (AMN) giao (SBD)=BI
Gọi K là giao điểm của BI với MN
=>K là giao điểm của MN với mp(SBD)
b: K là giao điểm của BI với MN
=>B,I,K thẳng hàng
d: ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường
=>O là trung điểm của AC và O là trung điểm của BD
Xét ΔSAC có
O,N lần lượt là trung điểm của CA,CS
=>ON là đường trung bình
=>ON//SA và ON=SA/2
Xét ΔINO và ΔIAS có
\(\widehat{INO}=\widehat{IAS}\)
\(\widehat{NIO}=\widehat{AIS}\)
Do đó: ΔINO đồng dạng với ΔIAS
=>\(\dfrac{IN}{IA}=\dfrac{NO}{AS}=\dfrac{1}{2}\)

a: \(N\in SC\subset\left(SCD\right)\)
\(N\in\left(ABN\right)\)
Do đó: \(N\in\left(SCD\right)\cap\left(ABN\right)\)
Xét (SCD) và (ABN) có
\(N\in\left(SCD\right)\cap\left(ABN\right)\)
CD//AB
Do đó: (SCD) giao (ABN)=xy, xy đi qua N và xy//AB//CD
c: Chọn mp(SAC) có chứa AN
Gọi O là giao điểm của AC và BD trong mp(ABCD)
\(O\in AC\subset\left(SAC\right)\)
\(O\in BD\subset\left(SBD\right)\)
Do đó: \(O\in\left(SAC\right)\cap\left(SBD\right)\)
mà \(S\in\left(SAC\right)\cap\left(SBD\right)\)
nên \(\left(SAC\right)\cap\left(SBD\right)=SO\)
Gọi K là giao điểm của AN với SO
=>K là giao điểm của AN với mp(SBD)

Đáp án A
Gọi O = A C ∩ B D , O ' = C M ∩ B D
Xét có S, J, O’ lần lượt thuộc 3 cạnh và thẳng hàng.
⇒ S O S I . J I J B . O ' B O ' O = 1 ⇔ 3 2 . J I J B .2 = 1 ⇔ 3 J I = J B
⇒ I B I J = 4

Trong mặt phẳng (SAC) : AF ∩S O = I là trọng tâm tam giác SBD ⇒ IA/IF=2
Đáp án B

Trong mặt phẳng (ABCD) : BD ∩ EC = K
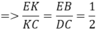
Trong mặt phẳng (SEC) : EF ∩ SK = J. Áp dụng định lí Me-nê-la-uýt vào tam giác EFC ta được: EJ/JF = 1
Đáp án B

Chứng minh B, J, I thẳng hàng. Áp dụng định lí Mê-nê-la-uýt vào tam giác IAB ta được IJ/JB = 1/4.
Đáp án C