Đồ thị (C): y = x + x - 2 có bao nhiêu điểm cực trị?
![]()
![]()
![]()
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án là B.
Hàm số dạng y = x - 1 2 - x có đạo hàm không đổi dấu trên từng khoảng xác định nên không có cực trị

Đáp án D.
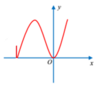
- Để vẽ đồ thị hàm số y = |f(x)| ta lấy đối xứng phần đồ thị hàm số nằm phía dưới trục hoành lên phía trên.
- Đồ thị hàm số y = |f(x)| có 3 điểm cực trị như hình vẽ:

Chọn D
+ Hàm phân thức hữu tỉ bậc nhất/ bậc nhất luôn đơn điệu trên các khoảng xác định của chúng,
do đó hàm này không có cực trị

Đặt h( x) = 2f( x) – ( x-1) 2
Suy ra đạo hàm: h’( x) = 2f’(x) -2( x-1).
Ta vẽ thêm đường thẳng y= x-1.
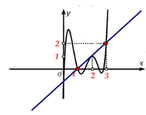
Ta có h’ (x) =0 khi f’(x) =x-1
Suy ra x=0; x=1; x=2; x=3
Theo đồ thị h’(x) > .0 khi f’(x) > x-1
Ta có :

Đồ thị hàm số g( x) có nhiều điểm cực trị nhất khi h( x) có nhiều giao điểm với trục hoành nhất.
Vậy đồ thị hàm số h( x) cắt trục hoành tại nhiều nhất 4 điểm, suy ra đồ thị hàm số g(x) có tối đa 7 điểm cực trị.
Chọn B.
Chọn D