Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đặt h( x) = 2f( x) – ( x-1) 2
Suy ra đạo hàm: h’( x) = 2f’(x) -2( x-1).
Ta vẽ thêm đường thẳng y= x-1.
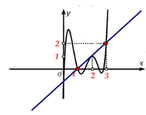
Ta có h’ (x) =0 khi f’(x) =x-1
Suy ra x=0; x=1; x=2; x=3
Theo đồ thị h’(x) > .0 khi f’(x) > x-1
Ta có :

Đồ thị hàm số g( x) có nhiều điểm cực trị nhất khi h( x) có nhiều giao điểm với trục hoành nhất.
Vậy đồ thị hàm số h( x) cắt trục hoành tại nhiều nhất 4 điểm, suy ra đồ thị hàm số g(x) có tối đa 7 điểm cực trị.
Chọn B.

Chọn D
+ Hàm phân thức hữu tỉ bậc nhất/ bậc nhất luôn đơn điệu trên các khoảng xác định của chúng,
do đó hàm này không có cực trị

Chọn đáp án C.
Ta có y ' = 3 x 2 - 2 ( m + 1 ) x + m 2 - 2
trước tiên ta phải có phương trình y ' = 0 có hai nghiệm phân biệt
![]()
![]()
Điều kiện hai điểm cực trị của đồ thị hàm số nằm cùng về một phía đối với trục hoành là y x 1 . y x 2 > 0
⇔ y = 0 có đúng một nghiệm thực.
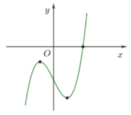
Thử trực tiếp các giá trị của m∈{−1,0,1,2} nhận các giá trị m∈{−1,0,2} để y = 0 có đúng một nghiệm thực.



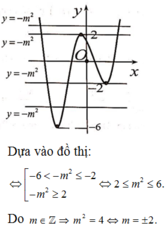
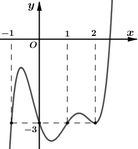
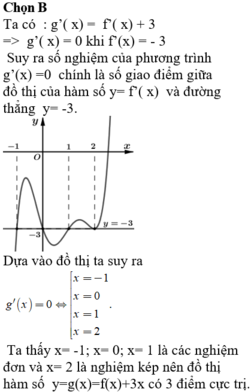
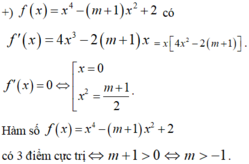
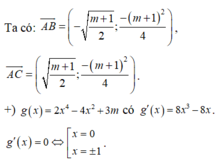

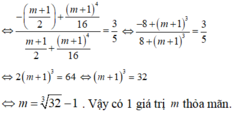
Chọn D