Cho hàm số f x = 2 x - 2 - x . Có bao nhiêu số nguyên m để bất phương trình f x 3 - 2 x 2 + 3 x - m + f 2 x - 2 x 2 - 5 < 0 có nghiệm đúng với mọi x ∈ 0 ; 1 .
A. 7.
B. 3.
C. 9.
D. 5.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

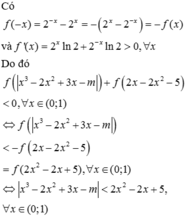
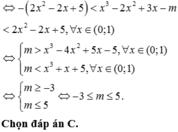

Lời giải:
Đặt $\sqrt{x^2+1}+x=a$ thì:
$f(a)=e^a-e^{\frac{1}{a}}$
$f'(a)=e^a+\frac{1}{a^2}.e^{\frac{1}{a}}>0$ với mọi $a$
Do đó hàm $f(a)$ là hàm đồng biến hay $f(x)$ là hàm đồng biến trên R
$\Rightarrow f(x)> f(0)=0$ với mọi $x>0$
$\Rightarrow f(\frac{12}{m+1})>0$ với $m$ nguyên dương
Do đó để $f(m-7)+f(\frac{12}{m+1})<0$ thì $f(m-7)<0$
$\Rightarrow m-7<0$
Mặt khác, dễ thấy: $f(x)+f(-x)=0$. Bây h xét:
$m=1$ thì $f(m-7)+f(\frac{12}{m+1})=f(-6)+f(6)=0$ (loại)
$m=2$ thì $f(m-7)+f(\frac{12}{m+1})=f(-5)+f(4)=f(4)-f(5)<0$ (chọn)
$m=3$ thì $f(m-7)+f(\frac{12}{m+1})=f(-4)+f(3)=f(3)-f(4)<0$ (chọn)
$m=4$ thì $f(m-7)+f(\frac{12}{m+1})=f(-3)+f(2,4)=f(2,4)-f(3)<0$ (chọn)
$m=5$ thì $f(m-7)+f(\frac{12}{m+1})=f(-2)+f(2)=0$ (loại)
$m=6$ thì $f(m-7)+f(\frac{12}{m+1})=f(-1)+f(12/7)>f(-1)+f(1)=0$ (loại)
Vậy có 3 số tm

Ta có: \(f'\left(x\right)=3x^2+2\ge2;\forall x\)
Đặt \(g\left(x\right)=f\left(f\left(x\right)\right)-x\Rightarrow g'\left(x\right)=f'\left(x\right).f'\left(f\left(x\right)\right)-1\ge2.2-1>0;\forall x\)
\(\Rightarrow g\left(x\right)\) đồng biến trên R
\(\Rightarrow\min\limits_{\left[2;6\right]}g\left(x\right)=g\left(2\right)=f\left(f\left(2\right)\right)-2\)
Ta cần tìm m để \(f\left(f\left(2\right)\right)-2\ge0\)
Đặt \(5^m=t\Rightarrow f\left(2\right)=12-t\)
\(\left(1\right)\Leftrightarrow\left(12-t\right)^3+2\left(12-t\right)-t-2\ge0\)
\(\Leftrightarrow\left(10-t\right)\left(t^2-26t+175\right)\ge0\)
\(\Rightarrow t\le10\)
\(\Rightarrow5^m\le10\Rightarrow m\le log_510\)

\(f^2\left(\left|x\right|\right)-\left(m-6\right)f\left(\left|x\right|\right)-m+5=0\) có \(a-b+c=0\) nên có các nghiệm \(\left[{}\begin{matrix}f\left(\left|x\right|\right)=-1\\f\left(\left|x\right|\right)=m-5\end{matrix}\right.\)
- Với \(f\left(\left|x\right|\right)=-1\Rightarrow\left|x\right|^2-4\left|x\right|+3=-1\Rightarrow\left|x\right|=2\Rightarrow x=\pm2\) có 2 nghiệm
- Xét \(f\left(\left|x\right|\right)=m-5\Leftrightarrow\left|x\right|^2-4\left|x\right|+8=m\) (1)
Từ BBT của \(y=\left|x\right|^2-4\left|x\right|+8\) dễ dàng suy ra (1) có 4 nghiệm pb khi \(4< m< 8\)
\(\Rightarrow m=\left\{5;6;7\right\}\) có 3 giá trị nguyên

Đáp án D
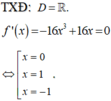
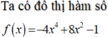
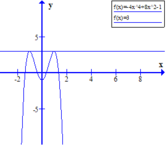
Dựa vào đồ thị suy ra có một giá trị nguyên dương của m để phương trình f(x)=m có đúng hai nghiệm phân biệt là m=3.

Ta có ![]()
Do đó hàm số f(x) đồng biến trên R. Với một hàm số f(x) đồng biến trên R ta có tính chất sau:
![]() Thật vậy
Thật vậy
+) Nếu ![]()
![]() (vô lí);
(vô lí);
+) Nếu ![]()
![]() (vô lí).
(vô lí).
+) Nếu ![]()
![]() (thỏa mãn)/
(thỏa mãn)/
Từ ba khả năng trên ta có điều phải chứng minh. Áp dụng tính chất này ta có:
![]()
![]()
![]()
Phương trình đã cho có ba nghiệm thực phân biệt khi và chỉ khi (*) có ba nghiệm thực phân biệt
![]()
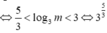
![]()
Có tất cả 20 số nguyên thỏa mãn.
Chọn đáp án A.

2: ĐKXĐ: x<>1
\(f'\left(x\right)=\dfrac{\left(x^2-3x+3\right)'\left(x-1\right)-\left(x^2-3x+3\right)\left(x-1\right)'}{\left(x-1\right)^2}\)
\(=\dfrac{\left(2x-3\right)\left(x-1\right)-\left(x^2-3x+3\right)}{\left(x-1\right)^2}\)
\(=\dfrac{2x^2-5x+3-x^2+3x-3}{\left(x-1\right)^2}=\dfrac{x^2-2x}{\left(x-1\right)^2}\)
f'(x)=0
=>x^2-2x=0
=>x(x-2)=0
=>\(\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
1:
\(f\left(x\right)=\dfrac{1}{3}x^3-2\sqrt{2}\cdot x^2+8x-1\)
=>\(f'\left(x\right)=\dfrac{1}{3}\cdot3x^2-2\sqrt{2}\cdot2x+8=x^2-4\sqrt{2}\cdot x+8=\left(x-2\sqrt{2}\right)^2\)
f'(x)=0
=>\(\left(x-2\sqrt{2}\right)^2=0\)
=>\(x-2\sqrt{2}=0\)
=>\(x=2\sqrt{2}\)

Đáp án B
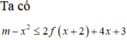
![]()
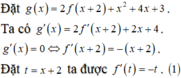
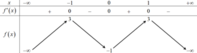
(1) là phương trình hoành độ giao điểm của đồ thị f'(t) và đường thẳng d : y = -t (hình vẽ)
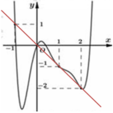
Dựa vào đồ thị của f'(t) và đường thẳng y =-t ta có


