Cho log a x = p , log b x = q , log a b c x = r . Hãy tính log c x theo p,q,r
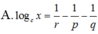
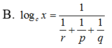
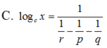
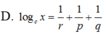
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hàm số \(y=log_cx\) nghịch biến
\(\Rightarrow0< c< 1\) và các hàm \(y=log_ax,y=log_bx\) đồng biến nên \(a,b>1\)
Ta chọn \(x=100\Rightarrow log_a>log_b100\Rightarrow a< b\Rightarrow b>a>c\)
\(\Rightarrow B\)

Vì \(\dfrac{1}{e}\simeq0,368< 1\)
\(\Rightarrow y=log_{\dfrac{1}{e}}\left(x\right)\) nghịch biến trên D = \(\left(0;+\infty\right)\)
Chọn C.
0<1/e<1
=>\(log_{\dfrac{1}{e}}\left(x\right)\) nghịch biến
=>C

Hàm số a,b là các hàm số logarit
a: \(log_{\sqrt{3}}x\)
Cơ số là \(\sqrt{3}\)
b: \(log_{2^{-2}}x\)
Cơ số là \(2^{-2}=\dfrac{1}{4}\)

ĐK: \(x>0\)
\(logx=2log5-log2\\ \Leftrightarrow logx=log25-log2\\ \Leftrightarrow logx=log\dfrac{25}{2}\Leftrightarrow x=12,5\)
Chọn C.

ĐKXĐ: \(x>0\)
\(log_{a^4}x-log_{a^2}x+log_ax=\frac{3}{4}\)
\(\Leftrightarrow\frac{1}{4}log_ax-\frac{1}{2}log_ax+log_ax=\frac{3}{4}\)
\(\Leftrightarrow\frac{3}{4}log_ax=\frac{3}{4}\)
\(\Leftrightarrow log_ax=1\)
\(\Rightarrow x=a\)
Chọn C