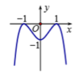
Đường cong trong hình sau là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phưng án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
A. y = - x 4 + 3 x 2 - 3
B. y = - x 4 + 2 x 2 - 1
C. y = - x 4 + x 2 - 1
D. y = - x 4 + 3 x 2 - 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B.
Dựa vào đồ thị thấy đây là đò thị của hàm số bậc bốn trùng phương y = a x 4 + b x 2 + c với hệ số a < 0 , b > 0 , c = - 1 nên loại đáp án A và D.
Hàm số đạt cực đại tại x = ± 1 nên chỉ có đáp án B thỏa mãn.
Đáp án C loại vì: y = - x 4 + x 2 - 1 ⇒ y ' = - 4 x 3 + 2 x
y ' = 0 ⇔ - 4 x 3 + 2 x = 0 ⇔ x = 0 x = 2 2 x = - 2 2

Chọn A
Đồ thị hàm số qua điểm có tọa độ (0;-1)
=> Loại C và D
Đồ thị hàm số qua điểm có tọa độ (1;0)
=> Loại B

Đáp án C
Phương pháp:
Quan sát đồ thị hàm số đã cho và nhận xét dựa trên dáng đồ thị các hàm số đa thức bậc 3, bậc 4.
Cách giải:
Đồ thị hàm số nhận (0;0) là điểm cực tiểu nên loại A, B, D.

Đáp án B
Dựa vào đồ thị hàm số ta có: lim x → + ∞ = + ∞ ⇒ a > 0
Đồ thị hàm số cắt trục Oy tại điểm 0 ; 2 ⇒ d = 2

Đáp án D.
Ta thấy đồ thị hàm số đã cho cắt trục tung tại điểm A(0; 2).
Do đó đồ thị ở đáp án D là đáp án duy nhất thỏa mãn đầu bài

Dựa vào các dạng đồ thị của hàm số bậc 3 ta loại đáp án B, C.
Đồ thị ứng ứng với hệ số a>0. Chọn C.

Ta thấy:
Tại x= 0 thì y = 0 . Do đó loại B và C.
Tại x = π thì y = -1. Thay vào hai đáp án còn lại chỉ có D thỏa mãn.
Chọn đáp án D.
Chọn B.
Dựa vào đồ thị thấy đây là đò thị của hàm số bậc bốn trùng phương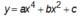 với hệ số a < 0, b > 0, c = -1 nên loại đáp án A và D.
với hệ số a < 0, b > 0, c = -1 nên loại đáp án A và D.
Hàm số đạt cực đại tại x = ± 1 nên chỉ có đáp án B thỏa mãn.
Đáp án C loại vì: