Tìm tất cả các giá trị thực của tham số a để tích phân ∫ 1 1 a 1 x x - 5 x - 4 d x tồn tại t...

K

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn lớp

Chọn môn

Mua vip

PT

Pham Trong Bach

20 tháng 1 2018

Tìm tất cả các giá trị thực của tham số a để tích phân ∫ 1 1 + a 1 x x - 5 x - 4 d x tồn tại ta được A. - 1 < a < 3 . B. a < - 1 . C. a ≠ 4 , a ≠ 5 . D. a < 3 ...

#Toán lớp 12

1

CM

Cao Minh Tâm

20 tháng 1 2018

Đáp án A

Những câu hỏi liên quan

PQ

Phan Quỳnh Gia

16 tháng 7 2021

Tìm tất cả các giá trị thực của tham số \(a\) để tích phân \(\int\limits^{1+a}_1\dfrac{1}{x\left(x-5\right)\left(x-4\right)}dx\) tồn tại

#Toán lớp 12

1

NV

Nguyễn Việt Lâm

Giáo viên

16 tháng 7 2021

Tích phân đã cho tồn tại khi hàm \(\dfrac{1}{x\left(x-5\right)\left(x-4\right)}\) xác định với mọi x thuộc \(\left[1;1+a\right]\) với \(a>0\) hoặc \(\left[1+a;1\right]\) với \(a< 0\)

ĐKXĐ: \(x\ne\left\{0;4;5\right\}\) hay \(x\in\left(-\infty;0\right)\cup\left(0;4\right)\cup\left(4;5\right)\cup\left(5;+\infty\right)\)

Do 2 khoảng \(\left[1;1+a\right]\) và \(\left[1+a;1\right]\) đều chứa số 1 nằm trong \(\left(0;4\right)\)

\(\Rightarrow\)Bài toán thỏa mãn khi \(\left[{}\begin{matrix}\left[1;a+1\right]\subset\left(0;4\right)\\\left[1+a;1\right]\subset\left(0;4\right)\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}1< 1+a< 4\\0< 1+a< 1\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}0< a< 3\\-1< a< 0\end{matrix}\right.\)

LC

Luong cong thanh

2 tháng 3 2021

1/ tìm tham số thực m để tồn tại x thỏa mãn f(x) = m^2x + 3 - ( mx + 4 ) âm. 2/ tìm tất cả các giá trị của m để f (x) = m( x-m ) - ( x - 1 ) không âm với mọi x thuộc ( - vô cực , m+1)

#Toán lớp 10

0

PT

Pham Trong Bach

19 tháng 8 2017

Tìm tất cả các giá trị thực của tham số a để tích phân ∫ 1 1 + a d x x x - 5 x - 4 tồn tại ta được

A. -1 < a < 3

B. a < -1

C. a ≠ 4 , a ≠ 5

D. a < 3

1

CM

Cao Minh Tâm

19 tháng 8 2017

Đáp án là A

PT

Pham Trong Bach

11 tháng 3 2018

Cho hàm số y = 2 x - 1 x - 1 có đồ thị (C). Tìm tất cả các giá trị thực của tham số m để đường thẳng d: y = x + m cắt (C) tại hai điểm phân biệt A, B sao cho AB = 4 A. m = -1 B. [ m = 0 m = 3 C. [ m = - 1 m = 3 D. m =...

1

CM

Cao Minh Tâm

11 tháng 3 2018

Đáp án C

Xét pt tương giao:

2 x - 1 x - 1 = x + m ⇔ 2 x - 1 - x + m x - 1 = 0 ⇔ x 2 - 3 - m x + m - 1 = 0

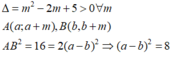
a + b 2 - 4 a b = 8 ⇔ 3 - m 2 - 4 1 - m = 8 ⇔ [ m = - 1 m = 3

PT

Pham Trong Bach

10 tháng 11 2017

Tìm tập S tất cả các giá trị thực của tham số m để tồn tại duy nhất cặp số (x;y) thỏa mãn log x 2 + y 2 + 2 4 x + 4 y - 6 + m 2 ≥ 1 và x 2 + y 2 + 2 x - 4 y + 1 = 0 . A. S = - 5 ; 5 B. S = - 7 ; - ...

1

CM

Cao Minh Tâm

10 tháng 11 2017

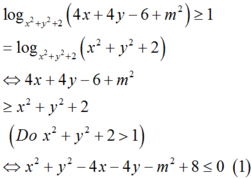
Ta có

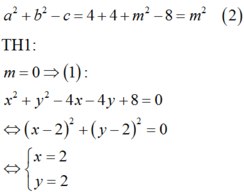
Cặp số x ; y = 2 ; 2 không thỏa mãn điều kiện .

Tập hợp các cặp số (x;y) thỏa mãn (1) là hình tròn C1(kể cả biên) tâm I1(2;2) bán kính R 1 = m .

Tập hợp các cặp số (x;y) thỏa mãn (2) là đường tròn C2 tâm I 2 - 1 ; 2 bán kính R 2 = 1 + 4 - 1 = 2 .

Để tồn tại duy nhất cặp số (x;y) thỏa mãn 2 điều kiện (1) và (2) Xảy ra 2 trường hợp sau:

TH1: C1; C2tiếp xúc ngoài

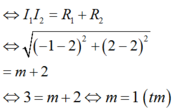
TH2: C1; C2 tiếp xúc trong và

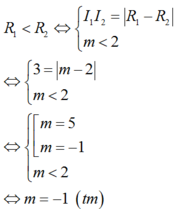
Vậy S = - 1 ; 1 .

Chọn D.

S

Shuu

22 tháng 8 2021

Câu 1 : Tìm tất cả các giá trị của tham số thực m để hàm số \(y=mx^3-2mx^2+\left(m-2\right)x+1\) không có cực trị

Câu 2: Tìm tất cả các giá trị thực của tham số m để hàm số \(y=\left(m-1\right)x^4-2\left(m-3\right)x^2+1\) không có cực đại

#Toán lớp 12

0

PT

Pham Trong Bach

23 tháng 4 2017

Tìm các giá trị thực của tham số a để hàm số f x = x - 2 + 3 k h i x ≥ 2 a x - 1 k h i x < 2 để tồn tại l i m x → 2 f x A. 2 B. 3 C. 4 D....

#Toán lớp 11

1

CM

Cao Minh Tâm

23 tháng 4 2017

Ta có:

lim x → 2 − f x = lim x → 2 − a x − 1 = 2 a − 1 lim x → 2 + f x = lim x → 2 + x − 2 + 3 = 3

Hàm số có giới hạn tại x=2 ⇔ lim x → 2 − f x = lim x → 2 + f x ⇔ 2 a − 1 = 3 ⇔ a = 2

Chọn đáp án A

PT

Pham Trong Bach

20 tháng 3 2018

Tìm tất cả giá trị của tham số thực m để đường thẳng d : y = x + m cắt đồ thị hàm số y = − x + 1 2 x − 1 tại hai điểm phân biệt A, B. A. m < 0 B. m ∈ ℝ C. m > 1 D. m = 5 ...

1

CM

Cao Minh Tâm

20 tháng 3 2018

Đáp án là B.

Phương trình hoàng độ giao điểm của

C & d : x + m 2 x − 1 = − x + 1 ; x ≠ 1 2

⇔ 2 x 2 + 2 m x − m − 1 = 0 (1)

C & d cắt nhau tại hai điểm phân biệt khi và chỉ khi phương trình (1) có hai nghiệm phân biệt và khác 1 2 .

Khi đó: m 2 + 2 m + 2 > 0 − 1 2 ≠ 0 ⇔ m ∈ ℝ .

PT

Pham Trong Bach

25 tháng 1 2018

Cho hàm số y = 2 x − 1 x − 1 có đồ thị (C). Tìm tất cả các giá trị thực của tham số m để đường thẳng d : y = x + m cắt (C) tại hai điểm phân biệt A, B sao cho AB = 4 A. m = − 1. B. m = 0 m = 3 . C. m = − 1 ...

1

CM

Cao Minh Tâm

25 tháng 1 2018

Đáp án C

Xét pt tương giao: