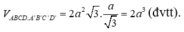Cho hình lăng trụ ABCD.A'B'C'D' có hình chiếu A' lên mp(ABCD) là trung điểm AB, ABCD là hình thoi cạnh 2a, góc A B C ^ = 60 ° , BB' tạo với đáy một góc 30 ° . Tính thể tích hình lăng trụ ABCD.A'B'C'D'.
A. a 3 3
B. 2 a 3 3
C. 2 a 3
D. a 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án là C
Gọi H là hình chiếu của A’ trên (ABCD). Dễ thấy góc
![]()
![]()
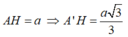
Dễ dàng tính được diện tích đáy

![]()

Đáp án D
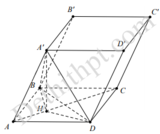
Gọi H là trung điểm của BC, kẻ H K ⊥ C ' D ' K ∈ C ' D '
Suy ra B H ⊥ A ' B ' C ' D ' ⇒ A C ' D ' ; A ' B ' C ' D ' ^ = B K H ^
Tam giác A’C’D’ đều cạnh 2 a ⇒ H K = d A ' ; C ' D ' = a 3
Tam giác BHK vuông tại H ⇒ B H = tan 60 ∘ x H K = 3 a
Diện tích hình thoi A’B’C’D’ là S A ' B ' C ' D ' = 2 a 2 3 .
Vậy thể tích khối lăng trụ ABC.A’B’C’D’ là V = B H . S A ' B ' C ' D ' = 3 a .2 a 2 3 = 6 3 a 3

Đáp án C
Ta có: A B C ^ = 120 ∘ ⇒ B A D ^ = 60 ∘ suy ra tam giác ABD là tam giác đều cạnh a. Khi đó A’.ABD là chóp đều cạnh đáy bằng a. Như vậy hình chiếu vuông góc của A’ lên mặt đáy trùng với trọng tâm tam giác ABD.
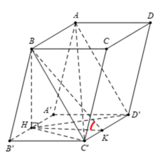
Ta có: A ' H = HA tan 60 ∘ = a 3 3 . 3 = a
⇒ V A ' A B D = 1 3 A ' H . S A B C = a 3 3 12
Do đó V A B C D . A ' B ' C ' D ' = 3 V A ' . A B C D = 6 V A ' A B D = a 3 3 2 .

Đáp án C
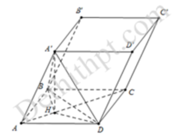
Ta có: A B C ^ = 120 ∘ ⇒ B A D ^ = 60 ∘ suy ra tam giác ABD là tam giác đều cạnh a. Khi đó A’.ABD là chóp đều cạnh đáy bằng a. Như vậy hình chiếu vuông góc của A’ lên mặt đáy trùng với trọng tâm tam giác ABD.
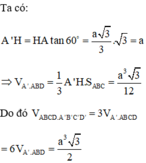

\(AH\perp\left(ABCD\right)\Rightarrow\widehat{A'AH}\) là góc giữa AA' và (ABCD) \(\Rightarrow\widehat{A'AH}=60^0\)
\(\Rightarrow AA'=\dfrac{AH}{cos60^0}=a\)
a. Ta có: \(\left\{{}\begin{matrix}A'H\perp\left(ABCD\right)\Rightarrow A'H\perp AD\\AD\perp AB\end{matrix}\right.\) \(\Rightarrow AD\perp\left(ABB'A'\right)\)
Mà \(AD\in\left(ADD'A'\right)\Rightarrow\left(ADD'A'\right)\perp\left(ABB'A'\right)\)
b. Kiểm tra lại đề câu này
Hai mặt phẳng (ABCD) và (A'B'C'D') hiển nhiên song song (theo tính chất lăng trụ) nên góc giữa chúng bằng 0. Do đó thấy ngay \(tan\left(\left(ABCD\right);\left(A'B'C'D'\right)\right)=0\)
Có lẽ không ai bắt tính điều này cả.
c.
\(\left(ABCD\right)||\left(A'B'C'D'\right)\Rightarrow d\left(A;\left(A'B'C'D'\right)\right)=d\left(A';\left(ABCD\right)\right)=A'H=a\)
Đáp án là A
+ Tính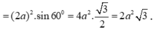
+ Tính A'H:
Ta có: ( Vì AH là hình chiếu của AA' trên mp(ABCD)).
( Vì AH là hình chiếu của AA' trên mp(ABCD)).
Suy ra: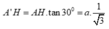
Vậy: