Cho hàm số f(x) có tập xác định là D f , đồ thị là (C). Mệnh đề nào dưới đây là đúng?
![]()

![]()
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D
Quan sát đồ thị hàm số y= f’( x)
+ Trên khoảng (0; 2) ta thấy đồ thị hàm số y= f’( x) nằm bên dưới trục hoành.
=> Trên khoảng (0; 2) thì f’( x) < 0.
=> Hàm số y= f( x) nghịch biến trên khoảng ( 0; 2) .

Chọn D.
Từ đồ thị của y=f’(x) ta có f’(x)<0 với xÎ(0;2). Suy ra f(x) nghịch biến trên khoảng (0;2)

Chọn A
+ Xét f’(x) = 0 khi x= -2; x= 0 hoặc x= 2.
+ Với x= -2: Giá trị của hàm số y= f’(x) đổi dấu từ âm sang dương khi qua x= -2
=> Hàm số y= f(x) đạt cực tiểu tại điểm x= -2.
+ Giá trị của hàm số y= f’(x) không đổi dấu khi đi qua x= 0 nên x= 0 không là điểm cực trị của hàm số.
+ Với x= 2: Giá trị của hàm số y= f’(x) đổi dấu từ dương sang âm khi qua x= 2
=> Hàm số y= f(x) đạt cực đại tại điểm x= 2.

Chọn A
Đồ thị của hàm số ![]() liên tục trên các đoạn
liên tục trên các đoạn ![]() và
và ![]() , lại có
, lại có ![]() là một nguyên hàm của
là một nguyên hàm của ![]() .
.
Do đó diện tích của hình phẳng giới hạn bởi các đường:
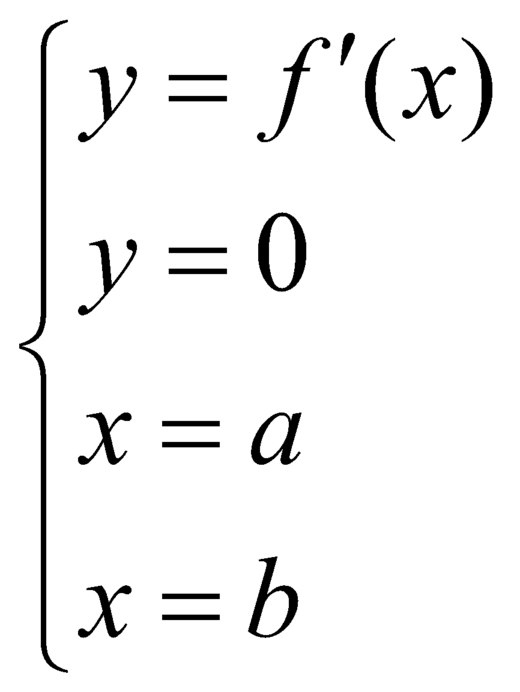 là:
là:
![]() .
.
Vì ![]()
![]()
Tương tự: diện tích của hình phẳng
giới hạn bởi các đường: 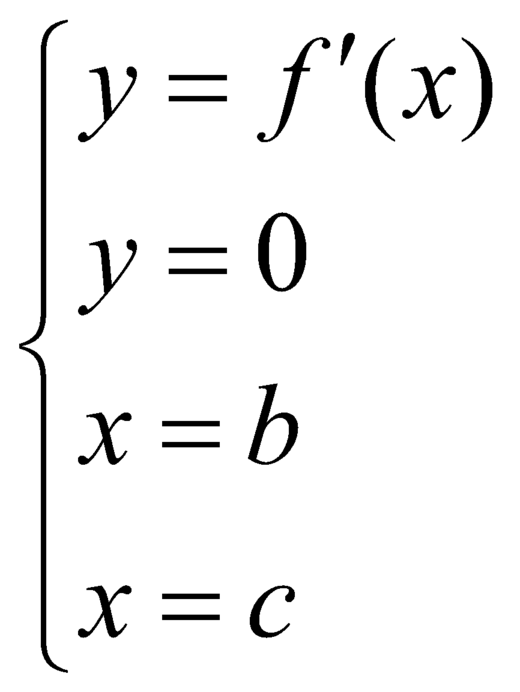 là:
là:
![]() .
.
![]()
![]() .
.
Mặt khác, dựa vào hình vẽ ta có: ![]()
![]() .
.
Từ (1), (2) và (3) ta chọn đáp án A.
( có thể so sánh ![]() với
với ![]() dựa vào dấu của
dựa vào dấu của ![]() trên đoạn
trên đoạn ![]() và so sánh
và so sánh ![]() với
với ![]() dựa vào dấu của
dựa vào dấu của ![]() trên đoạn
trên đoạn ![]() )
)

Đáp án C
Phương pháp:
+) ![]() đồng biến trên (a;b)
đồng biến trên (a;b)
+) ![]() nghịch biến trên (a;b)
nghịch biến trên (a;b)
Cách giải:
Quan sát đồ thị của hàm số y = f’(x), ta thấy:
+) ![]() đồng biến trên (a;b) => f(a) > f(b)
đồng biến trên (a;b) => f(a) > f(b)
+) ![]() nghịch biến trên (b;c) => f(b)<f(c)
nghịch biến trên (b;c) => f(b)<f(c)
Như vậy, f(a)>f(b), f(c)>f(b)
Đối chiếu với 4 phương án, ta thấy chỉ có phương án C thỏa mãn
Chọn C