Cho hình chóp S.ABCD có đáy ABCD là hình thang, A B / / B C , A D = 2 B C . Vẽ S S ' song song và bằng BC ta được hình đa diện mới S S ' A B C D . Khi đó V S S ' A B C D V S . A B C D bằng
A. 5/3
B. 3/2
C. 4/3
D. 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

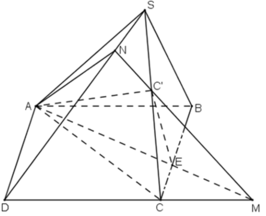
a) Giao điểm M của CD và mp(C’AE).
Trong mp(ABCD), d cắt CD tại M, ta có:
+ M ∈ CD
+ M ∈ d ⊂ (C’AE) ⇒ M ∈ (C’AE)
Vậy M là giao điểm của CD và mp(C’AE).
b) + Trong mặt phẳng (SCD), gọi giao điểm của MC’ và SD là N.
N ∈ MC’ ⊂ (C’AE) ⇒ N ∈ (C’AE).
N ∈ SD ⊂ (SCD) ⇒ N ∈ (SCD)
⇒ N ∈ (C’AE) ∩ (SCD).
⇒ (C’AE) ∩ (SCD) = C’N.
+ (C’AE) ∩ (SCB) = C’E.
+ (C’AE) ∩ (SAD) = AN.
+ (C’AE) ∩ (ABCD) = AE
Vậy thiết diện của hình chóp cắt bởi mặt phẳng (C’AE) là tứ giác C’NAE

Đáp án C
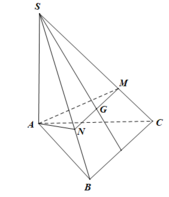
Qua G kẻ M N / / B C ( M ∈ S C , N ∈ S B )
V S . A M N V S . A B C = S A S A S M S B S N S C = 2 3 2 3 = 4 9 ⇒ V = 5 9 V S . A B C = 5 9 . 1 3 . S A . S A B C = 5 9 . 1 3 . a . 1 2 . a 2 = 5 a 3 54

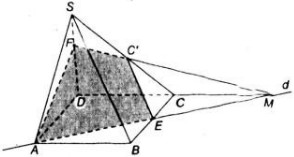
a) Trong (ABCD) gọi M = AE ∩ DC => M ∈ AE, AE ⊂ ( C'AE) => M ∈ ( C'AE). Mà M ∈ CD => M = DC ∩ (C'AE).
b)
Do M = DC ∩ (C'AE) nên M ∈ (SDC),.
Trong (SDC) : MC' ∩ SD = F.
Ta có:
\(\left(C'AE\right)\cap\left(SDC\right)=FC'\)
\(\left(C'AE\right)\cap\left(SAD\right)=AF\)
\(\left(C'AE\right)\cap\left(ABCD\right)=AE\)
\(\left(C'AE\right)\cap\left(SBC\right)=C'E\)
Vậy thiết diện là AEC'F.

Đáp án A

ABCD là hình thanh cân có AB = BC = CD = a; AD = 2a nên M là tâm của đáy ABCD.
SA = AD = 2a; SA ⊥ (ABCD) => tam giác SAD vuông cân tại A nên tâm mặt cầu ngoại tiếp hình chóp S.ABCD là trung điểm N của SD
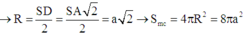

Chọn đáp án D
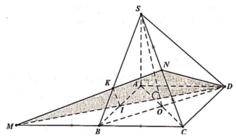
Gọi ![]()
Khi đó góc giữa 2 mặt phẳng (SBD) và (ABCD) bằng 45o![]()
Ta có: ∆BAD đều ![]()
Thể tích khối chóp S.ABCD bằng: 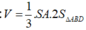
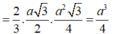
Ta có: N là trung điểm SC nên 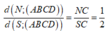
Thể tích khối chóp N.MCD bằng thể tích khối chóp N.ABCD bằng: ![]()
Ta có K là trọng tâm tam giác SMC
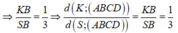
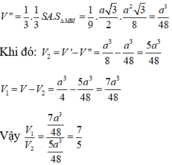
Đáp án C
Ta có V D . S S ' C = V D . S C B = V S . B C D
Mặt khác S B C D = 1 2 S A B D = 1 3 S A B C D
Do đó V D . S S ' C = V D . S C B = V S . B C D = 1 3 V S . A B C D
Khi đó V S S ' A B C D V S . A B C D = 1 3 + 1 1 = 4 3