Cho x và y là hai số nguyên cùng dấu thỏa mãn | x | + | y | = 75 . Tính giá trị biểu thức x + y.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

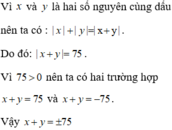

vì x và y cùng dấu nên ta có : \(\left|x\right|+\left|y\right|=\left|x+y\right|\)
do đó : \(\left|x+y\right|=12\)
vì : \(12\ge0\) nên ta có hai trường hợp : \(x+y=12\) và \(x+y=-12\)
vậy : \(x+y=\pm12\)

`x+y=3`
`<=>(x+y)^3=9`
`<=>x^2+2xy+y^2=9`
`<=>2xy+5=9`
`<=>2xy=4`
`<=>xy=2`
`<=>x^2-xy+y^2=3`
`=>M=(x+y)(x^2-xy+y^2)`
`=3.3`
`=9`

Biến đổi: 4 x 2 − 4 xy + y 2 = 0 ⇔ ( 2 x − y ) 2 = 0 ⇔ 2 x = y
Thay y = 2x vào P ta được P = -3

Ta có ( x + y ) 2 = x 2 + y 2 + 2 x y = 4 − 2 3 = ( 3 − 1 ) 2 ⇒ x + y = 3 − 1.
Suy ra P = x + y = 3 − 1 k h i x + y ≥ 0 1 − 3 k h i x + y < 0 .

cho hai số x,y thỏa mãn x+y=x.y=x/y, với y khác 0. Tính giá trị biểu thức P=2022x+2021y - Hoc24

\(ĐK:y\ne0\)
\(x+y=\dfrac{x}{y}\Leftrightarrow xy+y^2=x\)
Mà \(xy=x+y\Leftrightarrow x+y+y^2=x\)
\(\Leftrightarrow y\left(y+1\right)=0\Leftrightarrow y=-1\left(y\ne0\right)\\ \Leftrightarrow x-1=\dfrac{x}{-1}=-x\\ \Leftrightarrow2x-1=0\Leftrightarrow x=\dfrac{1}{2}\)
Vậy \(P=2022\cdot\dfrac{1}{2}+2021\left(-1\right)=1011-2021=-1010\)

\(P=\left(x^2+y^2\right)^2-2x^2y^2-4xy+3=\left[\left(x+y\right)^2-2xy\right]^2-2x^2y^2-4xy+3\)
\(=\left(16-2xy\right)^2-2x^2y^2-4xy+3=2x^2y^2-68xy+259\)
\(4=x+y\ge2\sqrt[]{xy}\Rightarrow0\le xy\le4\)
Đặt \(xy=a\Rightarrow0\le a\le4\)
\(P=2a^2-68a+259=259-2a\left(34-a\right)\le259\)
\(P_{max}=259\) khi \(a=0\) hay \(\left(x;y\right)=\left(4;0\right);\left(0;4\right)\)
\(P=\left(2a^2-68a+240\right)+19=2\left(4-a\right)\left(30-a\right)+19\ge19\)
\(P_{min}=19\) khi \(a=4\) hay \(x=y=2\)