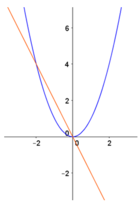
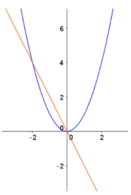
Cho a,b là hai số dương. Gọi K là hình phẳng nằm trong góc phần tư thứ hai, giới hạn bởi parabol y = a x 2 và đường thẳng y=-bx . Thể tích khối tròn xoay tạo được khi quay K xung quanh trục hoành là một số không phụ thuộc và giá trị của a và b nếu a và b thỏa mãn điều kiện sau:
![]()
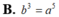
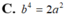
![]()

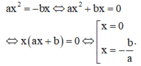
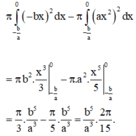


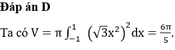
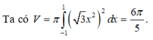
Chọn D