Cho hai số phức u, v thỏa mãn
3
u
-
6
i
+
3
u
-
1
-
3
i
=
5
10
,
v
-
1
+
2
i
=
v
¯
+
i
. Giá trị nhỏ nhất của
u
-
v
là: ...
Đọc tiếp
Cho hai số phức u, v thỏa mãn 3 u - 6 i + 3 u - 1 - 3 i = 5 10 , v - 1 + 2 i = v ¯ + i . Giá trị nhỏ nhất của u - v là:
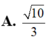
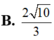
![]()
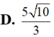

Đáp án B.