Làm bài 2 nha 
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


2:
a: \(A=\dfrac{x_1+x_2}{x_1x_2}=\dfrac{-6}{3}=-2\)
b: \(B=\dfrac{\left(x_1+x_2\right)^2-3x_1x_2}{1-x_1x_2}=\dfrac{36-3\cdot3}{1-3}=\dfrac{36-9}{-2}=-\dfrac{27}{2}\)
c: \(C=\sqrt{\left(x_1+x_2\right)^2-4x_1x_2}\)
\(=\sqrt{\left(-6\right)^2-4\cdot3}=2\sqrt{6}\)
d: \(D=\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)-3x_1x_2\)
\(=\left(-6\right)^3-3\cdot3\cdot\left(-6\right)-3\cdot3\)
=261

1, swimming
2,gardening
3,fishing/saiLing
4,drawing
5,music
7,photos
8,eggshells
Xin lỗi bn nhưng nếu điền từ b1 thì ko có từ phù hơp

Lê Nguyễn Ngọc Nhi bài tập này ở trong BÀI TẬP BỔ TRỢ VÀ NÂNG CAO TIENGS ANH 6 pải k?

\(1,\)
\(b,\)Để có hệ số góc bằng 3 thì \(m-1=3\Leftrightarrow m=4\)
\(2,\\ 1,\left\{{}\begin{matrix}x+4y=8\\2x+5y=13\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x+8y=16\\2x+5y=13\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}2x+5y=13\\3y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x+5=13\\y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=9\\y=1\end{matrix}\right.\\ 2,\\ a,B=\left[\dfrac{6}{a-1}+\dfrac{10-2\sqrt{a}}{\left(a-1\right)\left(\sqrt{a}-1\right)}\right]\cdot\dfrac{\left(\sqrt{a}-1\right)^2}{4\sqrt{a}}\\ B=\dfrac{6\sqrt{a}-6+10-2\sqrt{a}}{\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)^2}\cdot\dfrac{\left(\sqrt{a}-1\right)^2}{4\sqrt{a}}\\ B=\dfrac{4\sqrt{a}+4}{4\sqrt{a}\left(\sqrt{a}+1\right)}=\dfrac{\sqrt{a}+1}{\sqrt{a}\left(\sqrt{a}+1\right)}=\dfrac{1}{\sqrt{a}}=\dfrac{\sqrt{a}}{a}\)
\(b,C=B\left(a-\sqrt{a}+1\right)=\dfrac{\sqrt{a}\left(a-\sqrt{a}+1\right)}{a}=\dfrac{a\sqrt{a}-a+\sqrt{a}}{a}\\ C=\sqrt{a}-1+\dfrac{1}{\sqrt{a}}\ge2\sqrt{\sqrt{a}\cdot\dfrac{1}{\sqrt{a}}}-1=2-1=1\\ C_{min}=1\Leftrightarrow\sqrt{a}=\dfrac{1}{\sqrt{a}}\Leftrightarrow a=1\)

bài 1:
a) người trẻ, cân non.
b)muối mặn, màu áo đậm
còn lại mn ko bt nha![]()

4:
Cân nặng trung bình của 1 bạn là:
\(\dfrac{33,2+35+31,55+36,25}{4}=34\left(kg\right)\)
5:
Số lít dầu ở thùng 2 là:
\(31,7+10,5=42,2\left(lít\right)\)
Số lít dầu ở thùng 3 là:
\(\dfrac{10,5+42,2}{2}=26,35\left(lít\right)\)
Cả ba thùng có:
\(10,5+42,2+26,35=79,05\left(lít\right)\)

Bài 2:
a: Xét ΔBHA vuông tại H và ΔBHD vuông tại H có
BH chung
HA=HD
Do đó: ΔBHA=ΔBHD
b: Ta có: ΔBHA=ΔBHD
nên \(\widehat{ABH}=\widehat{DBH}\)
hay BH là tia phân giác của góc ABD

a) \(\sqrt{4x}+\sqrt{\dfrac{x}{4}}+\dfrac{1}{2}\sqrt{49x}=6\left(x\ge0\right)\)
\(\Rightarrow2\sqrt{x}+\dfrac{1}{2}\sqrt{x}+\dfrac{7}{2}\sqrt{x}=6\Rightarrow6\sqrt{x}=6\Rightarrow\sqrt{x}=1\Rightarrow x=1\)
b) ĐKXĐ: \(x\ge\dfrac{1}{2}\)
\(\sqrt{18x-9}-0,5\sqrt{2x-1}+\dfrac{1}{2}\sqrt{25\left(2x-1\right)}+\sqrt{49\left(2x-1\right)}=24\)
\(\Rightarrow\sqrt{9\left(2x-1\right)}-0,5\sqrt{2x-1}+\dfrac{5}{2}\sqrt{2x-1}+7\sqrt{2x-1}=24\)
\(\Rightarrow3\sqrt{2x-1}-0,5\sqrt{2x-1}+\dfrac{5}{2}\sqrt{2x-1}+7\sqrt{2x-1}=24\)
\(\Rightarrow12\sqrt{2x-1}=24\Rightarrow\sqrt{2x-1}=2\Rightarrow2x-1=4\Rightarrow x=\dfrac{5}{2}\)
c) \(\sqrt{x^2-2x+1}-7=0\Rightarrow\sqrt{\left(x-1\right)^2}=7\Rightarrow\left|x-1\right|=7\)
\(\Rightarrow\left[{}\begin{matrix}x-1=7\\x-1=-7\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=8\\x=-6\end{matrix}\right.\)
d) \(\dfrac{1}{2}\sqrt{\dfrac{49x}{x+2}}-3\sqrt{\dfrac{x}{4x+8}}-2\sqrt{\dfrac{x}{x+2}}-\sqrt{5}=0\left(\dfrac{x}{x+2}\ge0,x\ne-2\right)\)
\(\Rightarrow\dfrac{7}{2}\sqrt{\dfrac{x}{x+2}}-3\sqrt{\dfrac{x}{4\left(x+2\right)}}-2\sqrt{\dfrac{x}{x+2}}=\sqrt{5}\)
\(\Rightarrow\dfrac{7}{2}\sqrt{\dfrac{x}{x+2}}-\dfrac{3}{2}\sqrt{\dfrac{x}{x+2}}-2\sqrt{\dfrac{x}{x+2}}=\sqrt{5}\)
\(\Rightarrow0=\sqrt{5}\) (vô lý) \(\Rightarrow\) pt vô nghiệm
a) \(\sqrt{4x}+\sqrt{\dfrac{x}{4}}+\dfrac{1}{2}\sqrt{49x}=6\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\2\sqrt{x}+\dfrac{\sqrt{x}}{2}+\dfrac{7}{2}\sqrt{x}=6\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\\sqrt{x}\left(2+\dfrac{1}{2}+\dfrac{7}{2}\right)=6\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\6\sqrt{x}=6\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\\sqrt{x}=1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\x=1\end{matrix}\right.\) \(\Leftrightarrow x=1\)
Vậy \(S=\left\{1\right\}\)
b) \(\sqrt{18x-9}-0.5\sqrt{2x-1}+\dfrac{1}{2}\sqrt{25\left(2x-1\right)}+\sqrt{49\left(2x-1\right)}=24\)
\(\Leftrightarrow3\sqrt{2x-1}-0,5\sqrt{2x-1}+\dfrac{5}{2}\sqrt{2x-1}+7\sqrt{2x-1}=24\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x-1\ge0\\\sqrt{2x-1}\left(3-0.5+\dfrac{5}{2}+7\right)=49\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge\dfrac{1}{2}\\12\sqrt{2x-1}=24\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\ge\dfrac{1}{2}\\\sqrt{2x-1}=2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge\dfrac{1}{2}\\2x-1=4\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\ge\dfrac{1}{2}\\x=\dfrac{5}{2}\end{matrix}\right.\) \(\Leftrightarrow x=\dfrac{5}{2}\)
Vậy \(S=\left\{\dfrac{5}{2}\right\}\)
c) \(\sqrt{x^2-2x+1}-7=0\) (*)
Ta có \(x^2-2x+1=\left(x-1\right)^2\ge0\forall x\) \(\Rightarrow\sqrt{x^2-2x+1}\ge0\forall x\)
(*) \(\Leftrightarrow\sqrt{\left(x-1\right)^2}-7=0\)
\(\Leftrightarrow\left|x-1\right|-7=0\)
\(\Leftrightarrow x-1-7=0\)
\(\Leftrightarrow x=8\)
Vậy \(S=\left\{8\right\}\)
\(\)d) \(\dfrac{1}{2}\sqrt{\dfrac{49x}{x+2}}-3\sqrt{\dfrac{x}{4x+8}}-2\sqrt{\dfrac{x}{x+2}}-\sqrt{5}=0\) (**)
\(\Leftrightarrow\dfrac{7}{2}\sqrt{\dfrac{x}{x+2}}-\dfrac{3}{2}\sqrt{\dfrac{x}{x+2}}-2\sqrt{\dfrac{x}{x+2}}=\sqrt{5}\)
ĐKXĐ: \(\dfrac{x}{x+2}\ge0\) \(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x\ge0\\x+2>0\end{matrix}\right.\\\left\{{}\begin{matrix}x\le0\\x+2< 0\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x\ge0\\x>-2\end{matrix}\right.\\\left\{{}\begin{matrix}x\le0\\x< -2\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x\ge0\\x< -2\end{matrix}\right.\)
(**) \(\Leftrightarrow\sqrt{\dfrac{x}{x+2}}\left(\dfrac{7}{2}-\dfrac{3}{2}-2\right)=\sqrt{5}\)
\(\Leftrightarrow0\sqrt{\dfrac{x}{x+2}}=\sqrt{5}\)
\(\Leftrightarrow0=\sqrt{5}\) ( vô lý )
Vậy phương trình trên vô nghiệm


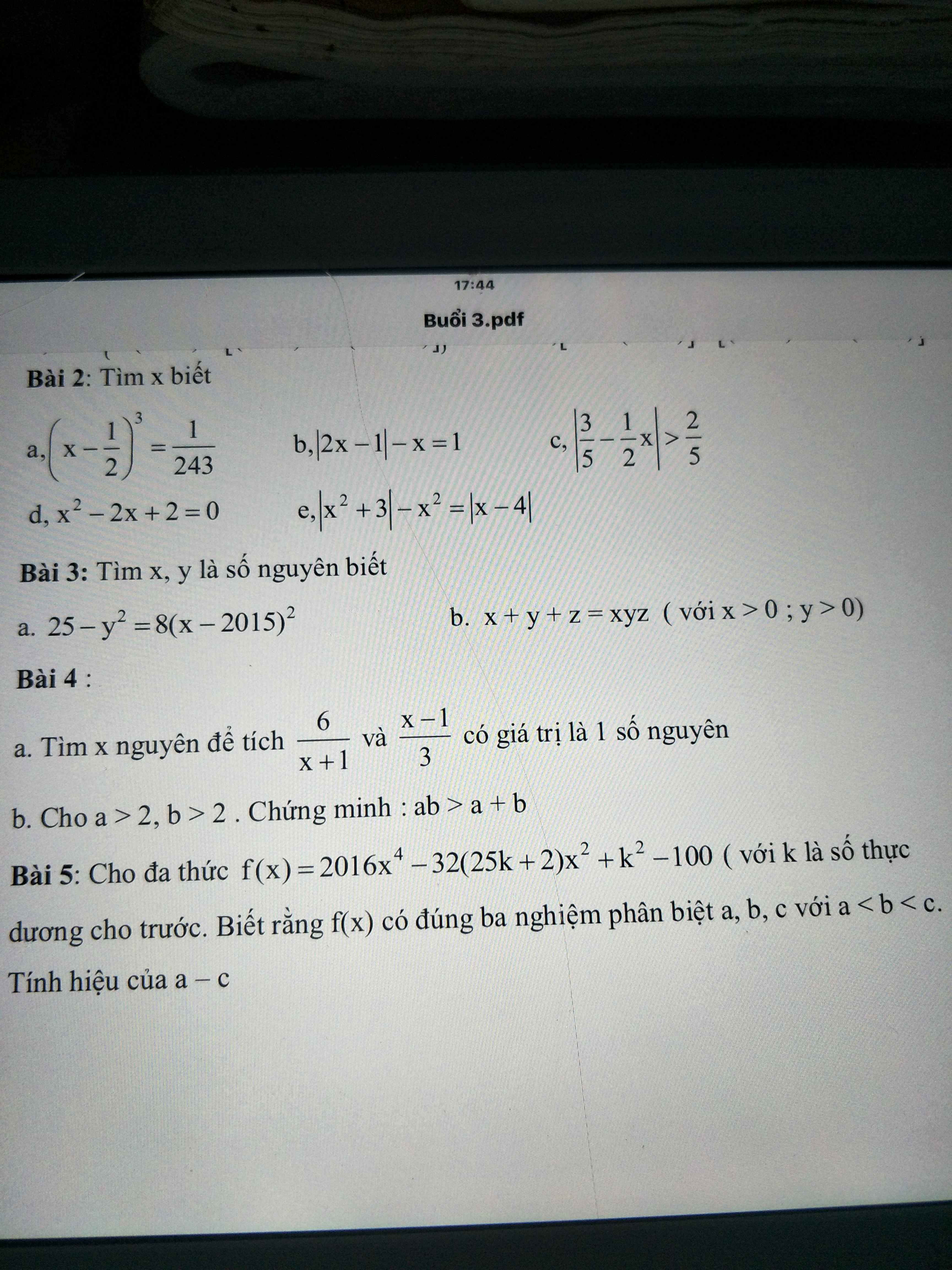
 Giúp mk bài 2; 3; 4; 5; 6 nha! Làm đc bài nào thì làm nha! Trang chơi lak tiếp theo của trang trên
Giúp mk bài 2; 3; 4; 5; 6 nha! Làm đc bài nào thì làm nha! Trang chơi lak tiếp theo của trang trên




