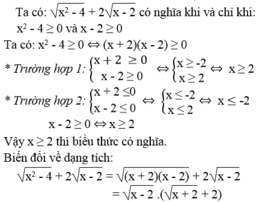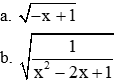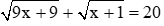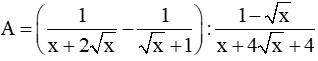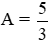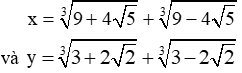Tìm điều kiện của x để các biểu thức sau có nghĩa và biến đổi chúng về dạng tích: 3 x + 3 + x 2 - 9
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
22 tháng 3 2017
Đúng(0)
Những câu hỏi liên quan
23 tháng 4 2017
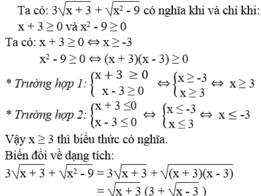
a. Biểu thức đã cho có nghĩa khi \(\sqrt{x^2-4}\) và \(\sqrt{x-2}\) đồng thời có nghĩa
* \(\sqrt{x^2-4}=\sqrt{\left(x-2\right)\left(x+2\right)}\) có nghĩa khi x \(x\le-2\) hoặc \(x \ge2\)
* \(\sqrt{x-2}\) có nghĩa khi \(x\ge2\)
Vậy điều kiện để biểu thức đã cho có nghĩa là \(x\ge2\)
Với điều kiện trên ta có:
\(\sqrt{x^2-4}+2\sqrt{x-2}=\sqrt{\left(x-2\right)\left(x+2\right)}+2\sqrt{x-2}=\sqrt{x-2}\left(\sqrt{x+2}+2\right)\)
13 tháng 8 2016
Bài 1:
a) \(ĐK:\begin{cases}x^2-4\ge0\\x-2\ge0\end{cases}\)\(\Leftrightarrow\begin{cases}x^2\ge4\\x-2\ge0\end{cases}\)\(\Leftrightarrow\begin{cases}x\ge2;x\ge-2\\x\ge2\end{cases}\)\(\Leftrightarrow x\ge2\)
\(\sqrt{x^2-4}+2\sqrt{x-2}=\sqrt{\left(x-2\right)\left(x+2\right)}-2\sqrt{x-2}=\sqrt{x-2}\cdot\left(\sqrt{x+2}-2\right)\)
b) \(ĐK;\begin{cases}x+3\ge0\\x^2-9\ge0\end{cases}\)\(\Leftrightarrow\begin{cases}x\ge-3\\x^2\ge9\end{cases}\)\(\Leftrightarrow\begin{cases}x\ge-3\\x\ge3;x\ge-3\end{cases}\)\(\Leftrightarrow x\ge3\)
\(3\sqrt{x+3}+\sqrt{x^2-9}=2\sqrt{x+3}+\sqrt{\left(x-3\right)\left(x+3\right)}=\sqrt{x+3}\left(2+\sqrt{x-3}\right)\)
13 tháng 8 2016
baif 2: a) \(\sqrt{x-5}=3\) diều kiện x>=5
pt<=> x-5=9<=>x=14 (thỏa)
b) \(\sqrt{x-10}=-2\) diều kiện x>=10
nhưng ta thầy VT>=0 mà VP<0=> pt trên vô nghiệm
c) \(\sqrt{2x-1}=\sqrt{5}\) diều kiện x>=1/2
pt<=>\(2x-1=5\)<=> x=3(thỏa)
d) \(\sqrt{4-5x}=12\) điều kiện x<=4/5
pt<=> 4-5x=144<=> x=-28 (loại)
Bài 1:a) điều kiện x^2-4>=0 và x-2>=0
<=> x<=-2,x>=2 và x>=2
=> điều kiện là x>=2
b)điều kiện x+3>=0 và x^2-9>=0
<=> x>=-3 và x<=-3, x>=3
=> điều kiện là > x>=3
CM
21 tháng 1 2017
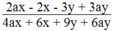xác định khi 4ax + 6x + 9y + 6ay
≠
0
⇒ 2x(2a + 3) + 3y(2a + 3) = (2a + 3)(2x + 3y) ≠ 0
Ta có: 2a + 3 ≠ 0 ⇒ a ≠ - 3/2 ; 2x + 3y ≠ 0 ⇒ x ≠ - 3/2 y
Điều kiện: x ≠ - 3/2 y và a ≠ - 3/2
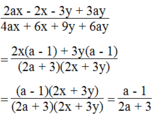
Vậy biểu thức không phụ thuộc vào x, y.
AT
14 tháng 7 2021
Để \(\sqrt{x^2+3}\) có nghĩa thì \(x^2+3\ge0\) (luôn đúng)
Để \(\sqrt{\left(x-1\right)\left(x+2\right)}\) có nghĩa thì \(\left(x-1\right)\left(x+2\right)\ge0\Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x-1\ge0\\x+2\ge0\end{matrix}\right.\\\left\{{}\begin{matrix}x-1\le0\\x+2\le0\end{matrix}\right.\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x\ge1\\x\le-2\end{matrix}\right.\)
14 tháng 7 2021
a) ĐKXĐ: \(x\in R\)
b) ĐKXĐ: \(\left[{}\begin{matrix}x\le-2\\x\ge1\end{matrix}\right.\)
13 tháng 8 2021
\(\left(\dfrac{x-3\sqrt{x}}{x-9}-1\right):\left(\dfrac{9-x}{x+\sqrt{x}-6}+\dfrac{\sqrt{x}-3}{\sqrt{x}-2}-\dfrac{\sqrt{x}-2}{\sqrt{x}+3}\right)\left(x\ge0;x\ne3;x\ne-3;x\ne9;x\ne4\right)\)
\(=\left(\dfrac{\sqrt{x}\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}-1\right):\left(\dfrac{9-x}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}+\dfrac{\sqrt{x}-3}{\sqrt{x}-2}-\dfrac{\sqrt{x}-2}{\sqrt{x}+3}\right)\\ =\dfrac{\sqrt{x}-\sqrt{x}-3}{\sqrt{x}+3}:\dfrac{9-x+\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)-\left(\sqrt{x}-2\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}\\ =\dfrac{-3}{\sqrt{x}+3}:\dfrac{9-x+x-9-x+4\sqrt{x}-4}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}\\ =\dfrac{-3}{\sqrt{x}+3}\cdot\dfrac{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}{-\left(\sqrt{x}-2\right)^2}\\ =\dfrac{3}{\sqrt{x}-2}\)
Tick hộ nha 😘
CM
28 tháng 6 2019
xác định khi:
(x + y)(6x – 6y)
≠
0 ⇒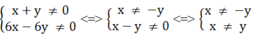 
Điều kiện x ≠ ± y
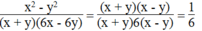
Vậy biểu thức không phụ thuộc vào x, y.
PT
1
2 tháng 11 2021
Bài 5:
\(x^3=18+3\sqrt[3]{\left(9+4\sqrt{5}\right)\left(9-4\sqrt{5}\right)}\left(\sqrt[3]{9+4\sqrt{5}}+\sqrt[3]{9-4\sqrt{5}}\right)\\ \Leftrightarrow x^3=18+3x\sqrt[3]{1}\\ \Leftrightarrow x^3-3x=18\\ y^3=6+3\sqrt[3]{\left(3-2\sqrt{2}\right)\left(3+2\sqrt{2}\right)}\left(\sqrt[3]{3+2\sqrt{2}}+\sqrt[3]{3-2\sqrt{2}}\right)\\ \Leftrightarrow y^3=6+3y\sqrt[3]{1}\\ \Leftrightarrow y^3-3y=6\\ P=x^3+y^3-3\left(x+y\right)+1993\\ P=\left(x^3-3x\right)+\left(y^3-3y\right)+1993\\ P=18+6+1993=2017\)