Gọi ∆ là tiếp tuyến của đường cong C : y = x 2 - x + 1 x + 1 . Biết rằng ∆ qua điểm (-1;0). Tính khoảng cách d từ điểm M(1;-1) đến ∆
A. d = 2 5
B. d = 1 5
C. d = 1
D. d = 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(y'=6x^2-4x-4\)
\(y'\left(0\right)=-4\)
\(y\left(0\right)=1\)
Do đó pt tiếp tuyến tại điểm có hoành độ x=0 là:
\(y=-4\left(x-0\right)+1\Leftrightarrow y=-4x+1\)

\(f'\left(x\right)=3x^2-6x+1\Rightarrow f'\left(1\right)=-2\)
Phương trình tiếp tuyến tại điểm có hoành độ bằng 1 là:
\(\Delta:y=f'\left(1\right)\left(x-1\right)+f\left(1\right)\Rightarrow y=\left(-2\right)\left(x-1\right)-2\)
Ta có y'=3x^2 - 6x +1
gọi M(x0;y0) là tiếp điểm
Ta có x0 =1 do đó yo =1^3 -3.1^2+1-1=-2
y'(1)=3.1^2-6.1+1=-2
Vậy phương trình tiếp tuyến của đồ thị (C) tại điểm có hoành độ bằng 1 là y=y'(1)(x-1)+(-2)=>y=-2x

Chọn A.
Tập xác định D = R \ {1}. Ta có 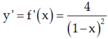
![]()
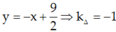
Vì tiếp tuyến vuông góc với Δ nên, ![]()
Gọi N(xo; yo) là tọa độ tiếp điểm của tiếp tuyến, ta có f’(xo) = ktt 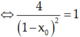
⇔ (xo – 1)2 = 4 ⇔ xo = 3 ∨ xo = -1.
Với xo = 3 ⇒ y = -5, phương trình tiếp tuyến tại điểm này là:
⇔ y = -1(x – 3) – 5 ⇔ y = -x – 2
Với xo = -1 ⇒ y = -1, phương trình tiếp tuyến tại điểm này là:
⇔ y = -1(x + 1) – 1 ⇔ y = -x – 2.
Đáp án D