cho tam giác abc vuông tại a vẽ phân giác BM (M thuộc ac). Trên BC lấy E sao cho AB=BE a)chứng minh ME vuông góc BC b)trên tia BA lấy D sao cho AD=EC. Chứng minh AE//DC
GIÚP MÌNH VỚI Ạ!!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔBAD và ΔBED có
BA=BE
góc ABD=góc EBD
BD chung
Do đo: ΔBAD=ΔBED
=>DA=DE
b,c: Xét ΔBFC có BA/AF=BE/EC
nên AE//FC
BA=BE
DA=DE
Do đó; BD là trung trực của AE
=>BD vuông góc với AE
=>BD vuông góc với FC
d: Xét ΔDAF vuông tại A và ΔDEC vuông tại E có
DA=DE
góc ADF=góc EDC
Do đó: ΔDAF=ΔDEC
=>góc ADF=góc EDC
=>góc ADF+góc ADE=180 độ
=>D,E,F thẳng hàng

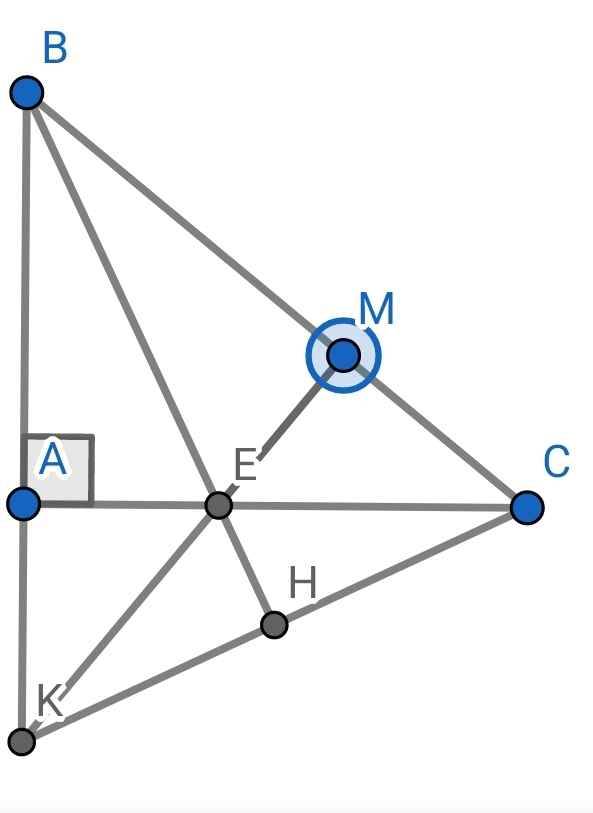
a) Xét ∆ABE và ∆MBE có:
BE chung
góc ABE = góc MBE (BE là phân giác của góc ABC)
AB = BM
⇒∆ABE = ∆MBE (c-g-c)
⇒góc BAE = góc BME (hai góc tương ứng)
⇒ME vuông góc BC
b) Do ∆ABE = ∆MBE (cmt)
⇒AE = ME (hai cạnh tương ứng)
Xét hai tam giác vuông: ∆AEK và ∆MEC có:
AE = ME (cmt)
góc AEK = góc MEC (đối đỉnh)
⇒∆AEK = ∆MEC (cạnh góc vuông - góc nhọn kề)
⇒EK = EC (hai cạnh tương ứng)
AK = MC (hai cạnh tương ứng)
Lại có: BK = BA + AK
BC = BM + MC
⇒BK = BC
c) Gọi H là giao điểm của BE và CK
Xét ∆BHK và ∆BHC có:
BK = BC (cmt)
góc HBK = góc HBC (do BE là tia phân giác của góc ABC)
BH chung
⇒∆BHK = ∆BHC (c-g-c)
⇒góc BHK = góc BHC (hai góc tương ứng)
Mà góc BHK + góc BHC = 180⁰ (kề bù)
⇒góc BHK = góc BHC = 180⁰ : 2 = 90⁰
⇒BH vuông góc KC
Hay BE vuông góc KC

Bài 3:
a: Xét ΔAIB và ΔCID có
IA=IC
góc AIB=góc CID
IB=ID
Do đó: ΔAIB=ΔCID
b: Xét tứ giác ABCD có
I là trung điểm chung của AC và BD
nên ABCD là hình bình hành
Suy ra: AD//BC va AD=BC
Bài 6:
a: Xét ΔADB và ΔAEC có
AD=AE
góc A chung
AB=AC
Do đó: ΔADB=ΔAEC
SUy ra: BD=CE
b: Xét ΔEBC và ΔDCB có
EB=DC
BC chung
EC=BD
Do đó: ΔEBC=ΔDCB
Suy ra: góc OBC=góc OCB
=>ΔOBC cân tại O
=>OB=OC
=>OE=OD
=>ΔOED cân tại O
c: Xét ΔABC có AE/AB=AD/AC
nên ED//BC

a: Xét ΔAMD vuông tại M và ΔAND vuông tại N có
AD chung
góc MAD=góc NAD
=>ΔMAD=ΔNAD
=>AM=AN
b: Xét ΔACB có AM/AB=AN/AC
nên MN//BC
c: Xét ΔADE có
AM vừa là đường cao, vừa là trung tuýen
=>ΔADE cân tại A
=>AD=AE
Xét ΔADF có
AN vừa là đường cao, vừa là trung tuyến
=>ΔADF cân tại A
=>AD=AF
=>AE=AF
=>ΔAEFcân tạiA

Sửa đề: ΔABC cân tại A
a:ΔABC cân tại A
mà AD là đường phân giác
nên AD là đường cao
=>AD vuông góc BC
b: Xét ΔAFI và ΔAEI có
AF=AE
góc FAI=góc EAI
AI chung
=>ΔAFI=ΔAEI
=>góc AFI=góc AEI
=>FI vuông góc AB
c: Xét ΔABC có
BE,AD là đường cao
BE cắt AD tại I
=>I là trực tâm
=>CI vuông góc AB
=>C,I,F thẳng hàng

a) Xét ΔABD và ΔEBD có
BA=BE(gt)
\(\widehat{ABD}=\widehat{EBD}\)(BD là tia phân giác của \(\widehat{ABE}\))
BD chung
Do đó: ΔABD=ΔEBD(c-g-c)
b) Ta có: ΔABD=ΔEBD(cmt)
nên \(\widehat{BAD}=\widehat{BED}\)(hai góc tương ứng)
mà \(\widehat{BAD}=90^0\)(gt)
nên \(\widehat{BED}=90^0\)
Xét ΔADM vuông tại A và ΔEDC vuông tại E có
DA=DE(ΔABD=ΔEBD)
\(\widehat{ADM}=\widehat{EDC}\)(hai góc đối đỉnh)
Do đó: ΔADM=ΔEDC(Cạnh góc vuông-góc nhọn kề)
Suy ra: AM=EC(Hai cạnh tương ứng)
c) Xét ΔBAE có BA=BE(gt)
nên ΔBAE cân tại B(Định nghĩa tam giác cân)
Suy ra: \(\widehat{BAE}=\widehat{BEA}\)(hai góc ở đáy)
mà \(\widehat{BAE}+\widehat{MAE}=180^0\)(hai góc kề bù)
và \(\widehat{BEA}+\widehat{AEC}=180^0\)(hai góc kề bù)
nên \(\widehat{AEC}=\widehat{EAM}\)

a: Xét ΔBAD và ΔBED có
BA=BE
góc ABD=góc EBD
BD chung
Do dó: ΔBAD=ΔBED
=>DA=DE
b: Sửa đề: BD vuông góc với AE
Ta có: BA=BE
DA=DE
Do đó; BD là trung trực của AE
=>BD vuông góc với AE
c: Xét ΔBFC có BA/AF=BE/EC
nên AE//CF
Xét tam giác ABM và tam giác NBM có:
AB = BN
góc ABM = góc NBM
BM chung
Nên: tam giác ABM = tam giác NBM
b, Ta có: AB = BN
=> Tam giác ABN là tam giác cân tai A
Xét tam giác cân ABN có:
BH là đường phân giác
=> BH đồng thời là đường trung tuyến
=> H là trung điểm của AN
=> HA = HN
c, Xét: tam giác cân ABN có:
BH là đường trung tuyến
=> BH đồng thời là đường cao
=> BH ⊥ AN
hay: HN ⊥ BM tại H
mặt khác ta có: CK ⊥ BM tại K
Nê: HN//CK (từ vuông góc đến //)
Cậu xem lại bài nhé!!!