Cho hai góc kề bù x O y ^ và y O z ^ . Hai tia Om, On lần lượt là các tia phân giác của hai góc x O y ^ và y O z ^ . Tìm số đo m O n ^
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
11 tháng 12 2018
Đúng(0)
Những câu hỏi liên quan
25 tháng 8 2021
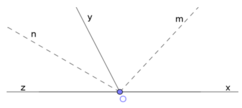
Ta có: \(\widehat{yOm}=\dfrac{\widehat{xOy}}{2}\)
\(\widehat{yOn}=\dfrac{\widehat{yOz}}{2}\)
Do đó: \(\widehat{yOm}+\widehat{yOn}=\dfrac{1}{2}\left(\widehat{xOy}+\widehat{yOz}\right)\)
\(\Leftrightarrow\widehat{mOn}=90^0\)
hay Om\(\perp\)On
10 tháng 6 2016
a) Ta có : góc xOy + góc yOz = 180o (kề bù)
=> \(\frac{1}{2}\) góc xOy + \(\frac{1}{2}\) góc yOz = 90o
=> góc yOm + góc yOn = 90o
hay góc mOn = 90o
b) Theo góc đối đỉnh ta có : góc yOm = góc y'Om' và góc xOy = góc zOy'
Mà góc yOm = \(\frac{1}{2}\) góc xOy (do Om là tia p/g của góc xOy) => góc y'Om' = \(\frac{1}{2}\) góc zOy'
Vậy Om là tia p/g của góc y'Oz
31 tháng 3 2016
\(yOn=nOz=\frac{1}{2}yOz\) (On là tia phân giác của góc yOz)
\(xOm=mOz=\frac{1}{2}xOz\) (Om là tia phân giác của góc xOz)
Ta có: \(yOz+xOz=180\) (2 góc kề bù)
Ta có: \(mOn=nOz+zOm=\frac{1}{2}yOz+\frac{1}{2}xOz=\frac{1}{2}\left(yOz+xOz\right)=\frac{1}{2}\times180=90\)
Vậy \(mOn=90\)