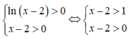Tập xác định của hàm số y = ln ( x - 2 ) π là
A . ℝ
B . ( 3 ; + ∞ )
C . ( 0 ; + ∞ )
D . ( 2 ; + ∞ )
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
9 tháng 6 2019
Chọn C
Hàm số y = ln ( x 2 - 2 x - m + 1 ) có tập xác định là ℝ khi và chỉ khi:
CM
6 tháng 9 2018
Chọn C.
Phương pháp: Viết điều kiện xác định và giải điều kiện đó.
HQ
Hà Quang Minh
Giáo viên
24 tháng 8 2023
\(a,4^x-2^{x+1}\ge0\\ \Leftrightarrow2^{x+1}\le2^{2x}\\ \Leftrightarrow x+1\le2x\\ \Leftrightarrow x\ge1\)
Tập xác định của hàm số là D = \([1;+\infty)\)
\(b,\left\{{}\begin{matrix}x>0\\1-ln\left(x\right)>0\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x>0\\ln\left(x\right)< 1\end{matrix}\right.\\ \Leftrightarrow0< x< e\)
Tập xác định của hàm số là \(\left(0;e\right)\)
HQ
Hà Quang Minh
Giáo viên
24 tháng 8 2023
a, \(y=log\left|x+3\right|\) có nghĩa khi \(\left|x+3\right|>0\)
Mà \(\left|x+3\right|\ge0\forall x\in R\)
\(\Rightarrow\) \(\left|x+3\right|>0\) khi \(x\ne-3\)
Vậy tập xác định của hàm số là D = R \ {-3}.
b, \(y=ln\left(4-x^2\right)\) có nghĩa khi \(4-x^2>0\)
\(\Rightarrow x^2< 4\\ \Leftrightarrow-2< x< 2\)
Vậy tập xác định của hàm số là D = (-2;2).
CM
30 tháng 10 2019
Chọn D
Hàm số y= cot(2x-π/3)+2 xác định khi và chỉ khi sin(2x-π/3)≠0
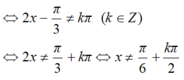
Chọn B
ĐKXĐ: