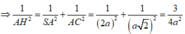Cho hình chóp S.ABCD có đường cao SA = 2a, đáy ABCD là hình thang vuông ở A và D. AB = 2a, AD = CD = a. Khoảng cách từ điêm A đến mặt phẳng (SBC) bằng
A. 2 a 3
B. 2 a 2
C. 2 a 3
D. a 2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
15 tháng 3 2018
Đáp án là A
Gọi K là trung điểm AB => KA=KB=a
Dễ thấy tứ giác ADCK là hình vuông => CK=a
Tam giác ACB có trung tuyến C K = 1 2 A B Þ Tam giác ACB vuông tại C
Trong (SAC), từ A hạ AH ⊥ SC tại H =>AH ⊥ (SBC)
Tam giác SAC vuông tại A
1 tháng 6 2021
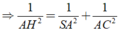
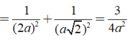
a, Ta có: \(\left\{{}\begin{matrix}AB\perp SA\left(do:SA\perp\left(ABCD\right)\right)\\AB\perp AD\left(gt\right)\end{matrix}\right.\)
\(\Rightarrow AB\perp\left(SAD\right)\)
Từ C kẻ CH // AB ⇒ CH ⊥ (SAD)
⇒ d (C, (SAD)) = CH = 2a
b, Ta có: \(\left(SAC\right)\cap\left(ABCD\right)=AC\)
Hạ DE ⊥ AC ⇒ DE ⊥ (SAC)
⇒ d(D, (SAC)) = DE
Ta có: AC = 2a√2, AH = HC 2a và HD = a
Xét tam giác HDC vuông tại H, có: \(DC=\sqrt{HD^2+HC^2}=a\sqrt{5}\)
Xét tam giác AHC vuông cân tại H, có: \(\widehat{HAC}=45^o=\widehat{DAE}\)
Xét tam giác ADE vuông tại E, có: \(DE=AD.sin\widehat{DAE}=\dfrac{3a\sqrt{2}}{2}\)
CM
2 tháng 7 2018
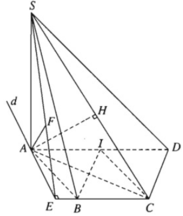
a) Vì ABCD là nửa lục giác đều nội tiếp trong đường tròn đường kính AD = 2a nên ta có: AD //BC và AB = BC = CD = a, đồng thời AC ⊥ CD, AB ⊥ BD, AC = BD = a√3.
Như vậy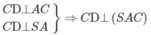 
Trong mặt phẳng (SAC) dựng AH ⊥ SC tại H ta có AH ⊥ CD và AH ⊥ SC nên AH ⊥ (SCD)
Vậy AH = d(A,(SCD))
Xét tam giác SAC vuông tại A có AH là đường cao, ta có:
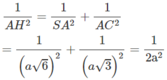
Vậy A H 2 = 2 a 2 ⇒ A H = a 2
Gọi I là trung điểm của AD ta có BI // CD nên BI song song với mặt phẳng (SCD). Từ đó suy ra d(B, (SCD)) = d(I,(SCD)).
Mặt khác AI cắt (SCD) tại D nên
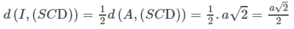
Do đó: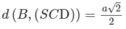 
b) Vì AD // BC nên AD // (SBC), do đó d(AD, (SBC)) = d(A,(SBC))
Dựng AD ⊥ BC tại E ⇒ BC ⊥ (SAE)
Dựng AD ⊥ SE tại F ta có:
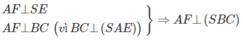
Vậy AF = d(A,(SBC)) = d(AD, (SBC))
Xét tam giác vuông AEB ta có:
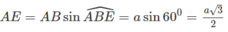
Xét tam giác SAE vuông tại A ta có:
NV
Nguyễn Việt Lâm
Giáo viên
29 tháng 4 2021
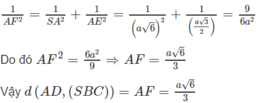
Bạn kiểm tra lại đề,
1. ABCD là hình thang vuông tại A và B hay A và D? Theo dữ liệu này thì ko thể vuông tại B được (cạnh huyền DC nhỏ hơn cạnh góc vuông AB là cực kì vô lý)
2. SC và AC cắt nhau tại C nên giữa chúng không có khoảng cách. (khoảng cách bằng 0)
29 tháng 4 2021
Nguyễn Việt Lâm
e xin loi a
ABCD là hình thang vuông tại A và D
còn đoạn sau khoảng cách giữa 2 đt SC và AC thì e kh biet no sai o đau
anh giup em vs ah
Chọn A.
Gọi K là trung điểm AB => AK = KB = a
Dễ thấy tứ giác ADCK là hình vuông => CK = a
∆ ACB có trung tuyến CK = 1 2 AB => ∆ ACB vuông tại C.
Ta có: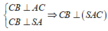
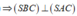
Trong (SAC) từ A hạ AH ⊥ SC tại H => AH ⊥ (SBC)
∆ SAC vuông tại A