Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án là A

Gọi K là trung điểm AB => KA=KB=a
Dễ thấy tứ giác ADCK là hình vuông => CK=a
Tam giác ACB có trung tuyến C K = 1 2 A B Þ Tam giác ACB vuông tại C

![]()
Trong (SAC), từ A hạ AH ⊥ SC tại H =>AH ⊥ (SBC)
Tam giác SAC vuông tại A
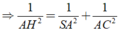
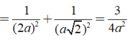


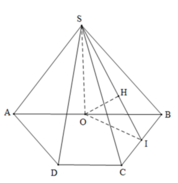
\(\begin{cases}\left(SIB\right)\perp\left(ABCD\right)\\\left(SIC\right)\perp\left(ABCD\right)\end{cases}\) \(\Rightarrow SI\perp\left(ABCD\right)\)
Kẻ \(IK\perp BC\left(K\in BC\right)\Rightarrow BC\perp\left(SIK\right)\)\(\Rightarrow\widehat{SKI}=60^0\)
Diện tích hình thang ABCD : \(S_{ABCD}=3a^2\)
Tổng diện tích các tam giá ABI và CDI bằng \(\frac{3a^2}{2}\) Suy ra \(S_{\Delta IBC}=\frac{3a^2}{2}\)
\(BC=\sqrt{\left(AB-CD\right)^2+AD^2}=a\sqrt{5}\)
\(\Rightarrow IK=\frac{2S_{\Delta IBC}}{BC}=\frac{3\sqrt{5}a}{5}\)
\(\Rightarrow SI=IK.\tan\widehat{SKI}=\frac{3\sqrt{15}a}{5}\)
Thể tích của khối chóp S.ABCD : \(V=\frac{1}{3}S_{ABCD}.SI=\frac{3\sqrt{15}a^2}{5}\)

Chọn D.
Cách 1:

Gọi M là trung điểm của CD, ABMD là hình vuông cạnh bằng 1.
BM= 1 2 DC tam giác BCD vuông cân tại B.
Ta có:
![]()
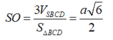
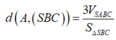
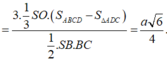
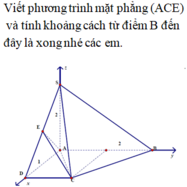
Cách 2: Gọi M là trung điểm của CD, H là trung điểm của BD
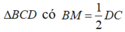
=> Tam giác BCD vuông tại B.
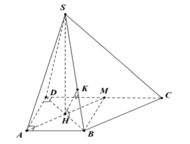
![]()
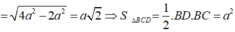
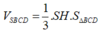
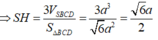
+) Ta có: AH // (SBC)
![]()
![]()
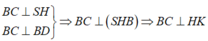
Do đó
![]()
Tam giác SHB có
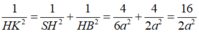
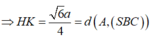

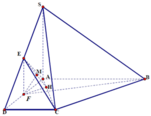
kẻ CH_|_AD. AD=AH+HD= BC+căn ( CD^2- CH^2). Thay số.
V=1/3. SA. S abcd
Sabcd=1/2.( BC+ AD).AB
d( D; ( SBC))=d( A;(SBC))=AK
kẻ AK _|_ SB


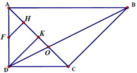
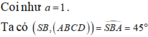


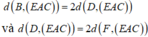
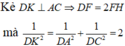

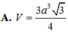
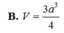
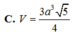
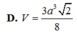



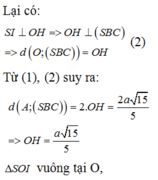
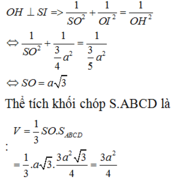
Chọn A.
Gọi K là trung điểm AB => AK = KB = a
Dễ thấy tứ giác ADCK là hình vuông => CK = a
∆ ACB có trung tuyến CK = 1 2 AB => ∆ ACB vuông tại C.
Ta có: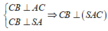
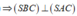
Trong (SAC) từ A hạ AH ⊥ SC tại H => AH ⊥ (SBC)
∆ SAC vuông tại A