Cho hình lập phương ABCD.A'B'C'D' . Gọi α là góc giữa đường thẳng AC’ với mặt phẳng (ABCD) . Mệnh đề nào dưới đây đúng?
A. 2 π 9 ≤ α ≤ π 4
B. π 4 < α < π 3
C. π 6 < α < 2 π 9
D. π 9 ≤ α ≤ π 6
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C.

Ta có AC là hình chiếu vuông góc của A'C trên mặt phẳng (ABCD).
Lại do CC' ⊥ (ABCD) nên tam giác C'AC vuông tại C
Suy ra
![]()
Ta có
![]()
Phân tích phương án nhiễu
Phương án A: Sai do HS tính được tan α 2 2 và cho rằng α = π 4
Phương án B: Sai do HS tính sai
tan
α
=
A
C
A
C
'
=
2
nên suy ra ![]()
Phương án D: Sai do HS tính sai tan α = C C ' A C ' = 3 3 nên suy ra α = π 6

Chọn C.
Ta có :
P = sin(π + α).cos(π - α) = -sin α.(-cos α) = sin α.cos α.
Và ![]() = cos α.(-sin α) = -sin α.cos α.
= cos α.(-sin α) = -sin α.cos α.
Do đó; P + Q = 0.

Đáp án D
Gọi I là giao điểm của AC và BD
A I ⊥ B D A I ⊥ B B ' ⇒ A I ⊥ ( B B ' D ' D ) ⇒ B’I là hình chiếu vuông góc của AB’ lên (BB’D’D)
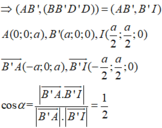
Đáp án C
Ta có AC là hình chiếu vuông góc của AC' trên mặt phẳng (ABCD) .
Lại do C C ' ⊥ A B C D nên tam giác C'AC vuông tại C .
Suy ra A C ' , A B C D = A C ' , A C = C ' A C = α .
Ta có tan α = C C ' A C = 2 2 ⇒ π 6 < α < 2 π 9 .
Phân tích phương án nhiễu
Phương án A: Sai do HS tính được tan α 2 2 và cho rằng α = π 4 .
Phương án B: Sai do HS tính sai tan α = A C A C ' = 2 nên suy ra π 4 < α < π 3 .
Phương án D: Sai do HS tính sai tan α = C C ' A C ' = 3 3 nên suy ra α = π 6 .