Tìm x, y thuộc Z biết (2x + 1)(3y - 2) = -55
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
BT
3 tháng 3 2017
=> 2x=\(\frac{-55-\left(3y-2\right)}{\left(3y-2\right)}=-1-\frac{55}{\left(3y-2\right)}\)
Để 2x nguyên => 3y-2 là ước của 55 => 3y-2 thuộc {-55; -11; -5; -1; 1; 5; 11; 55}
+/ 3y-2=-55 => y=-53/3 => Loại
+/ 3y-2=-11 => y=-9/3=-3 => x=(\(-1-\frac{55}{-11}\)):2=2
+/ 3y-2=-5 => y=-3/3 =-1=> x=5
+/ 3y-2=5 => y=7/3 => Loại
+/ 3y-2=11 => y=13/3 => Loại
+/ 3y-2=1 => y=3/3=1 => x=-56:2=-28
+/ 3y-2=-55 => y=-53/3 => Loại
+/ 3y-2=55 => y=57/3=19 => x=-1
ĐS Các cặp x, y nguyên thỏa mãn là: {2; -3}; {5; -1}; {-28; 1}; {-1; 19}
15 tháng 11 2015
2x(3y - 2 ) + ( 3y - 2 ) = -55
( 3y- 2 )( 2x + 1 ) = -55
TA có : -55 = -1.55 = -55.1 = 11.-5 = -5.11
(+) 3y - 2 = -1 và 2x+ 1 = 55
=> 3y = 1 và 2x = 54 ( loại)
(+) 3y- 2 = -55 và 2x + 1 = 1
=> 3y = - 53 và 2x = 0 ( loại)
(+) 3y - 2 = 11 và 2x + 1 = -5
=> 3y = 13 (loại ) 2x = -6
(+) 3y - 2 = -11 và 2x + 1 = 5
=> 3y = -9 và 2x = 4
=> y = -3 và x = 2
VẬy x= 2 ; y = -3
CM
4 tháng 5 2019
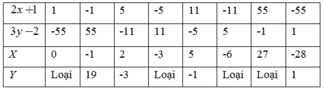
a) ( 2 x + 1 ) ( 3 y − 2 ) = − 55
Suy ra ( 2 x + 1 ) v à ( 3 y − 2 ) ∈ Ư ( - 55 ) = 1 ; − 1 ; 5 ; − 5 ; 11 ; − 11 ; 55 ; − 55
Khi đó ta có bảng sau:
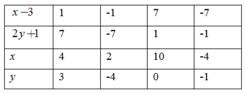
b) ( x − 3 ) ( 2 y + 1 ) = 7
Suy ra ( x − 3 ) và ( 2 y + 1 ) ∈ Ư ( 7 ) = 1 ; − 1 ; 7 ; − 7
Khi đó ta có bảng sau
c) y ( y 4 + 12 ) = − 5
Suy ra ( y 4 + 12 ) ∈ Ư ( - 5 ) = 1 ; − 1 ; 5 ; − 5
Vì y 4 ≥ 0 ⇒ y 4 + 12 ≥ 12 ⇒ không có giá trị của y thỏa mãn ycbt.
BT
1
14 tháng 3 2018
2x(3y-2)+(3y-2)=-55
3y-2(2x+1)=-55
TH1: 3y-2(2x+1)=(-5).11
=> \(\hept{\begin{cases}3y-2=-5\\2x+1=11\end{cases}}\)hoặc \(\hept{\begin{cases}3y-2=11\\2x+1=-5\end{cases}}\)
=> \(\hept{\begin{cases}y=-1\\x=5\end{cases}}\)hoặc \(\hept{\begin{cases}y=\frac{13}{3}\\x=-3\end{cases}}\)(không thỏa mãn do x;y\(\in Z\))
=> \(\hept{\begin{cases}y=-1\\x=5\end{cases}}\)(1)
TH2: 3y-2(2x+1)=5.(-11)
=> \(\hept{\begin{cases}3y-2=5\\2x+1=-11\end{cases}}\)hoặc \(\hept{\begin{cases}3y-2=-11\\2x+1=5\end{cases}}\)
=> \(\hept{\begin{cases}y=\frac{7}{3}\\x=-6\end{cases}}\)(không thỏa mãn do x;y \(\in Z\)) hoặc \(\hept{\begin{cases}y=-3\\x=2\end{cases}}\)
=> \(\hept{\begin{cases}y=-3\\x=2\end{cases}}\)(2)
TH3: 3y-2(2x+1)=(-1).55
=> \(\hept{\begin{cases}3y-2=-1\\2x+1=55\end{cases}}\)hoặc \(\hept{\begin{cases}3y-2=55\\2x+1=-1\end{cases}}\)
=> \(\hept{\begin{cases}y=\frac{1}{3}\\x=27\end{cases}}\)(không thỏa mãn do x;y\(\in Z\)) Hoặc \(\hept{\begin{cases}y=19\\x=-1\end{cases}}\)
=> \(\hept{\begin{cases}y=19\\x=-1\end{cases}}\)(3)
TH4: 3y-2(2x+1)=1.(-55)
=> \(\hept{\begin{cases}3y-2=1\\2x+1=-55\end{cases}}\)hoặc \(\hept{\begin{cases}3y-2=-55\\2x+1=1\end{cases}}\)
=> \(\hept{\begin{cases}y=1\\x=-27\end{cases}}\)hoặc \(\hept{\begin{cases}y=\frac{-53}{3}\\x=0\end{cases}}\)(không thỏa mãn)
=> \(\hept{\begin{cases}y=1\\x=-27\end{cases}}\)(4)
Từ (1),(2),(3) và (4) => \(\hept{\begin{cases}y=-1\\x=5\end{cases}}\);\(\hept{\begin{cases}y=-3\\x=2\end{cases}}\);\(\hept{\begin{cases}y=19\\x=-1\end{cases}}\);\(\hept{\begin{cases}y=1\\x=-27\end{cases}}\)
TH
0
KK
1
6 tháng 2 2018
a) Do (x-3).(2y+1)=7
nên (x-3),(2y+1) thuộc Ư(7)
mà Ư(7)={1;-1;7;-7}
mà 2y+1 là số nguyên lẻ
nên x-3 thuộc {1;-1;7;-7}
2y+1 thuộc {7;-7;1;-1}
nên x thuộc {4;2;10;-4}
2y thuộc {6;-8;0;-2}= y thuộc {3;-4;0;-1}
NT
0
(2x+1).(3y-2)=55