Tập nghiệm của bất phương trình 2 x > 4 x + 6 là
A. - ∞ ; - 6
B. - ∞ ; - 12
C. 6 ; + ∞
D. 12 ; + ∞
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

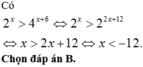

hoc gioi the hihiihihihhhihihihihiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiii
,mnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnn


\(\dfrac{x^2+x+3}{x^2-4}\ge1\Leftrightarrow\dfrac{x^2+x+3}{x^2-4}-1\ge0\)
\(\Leftrightarrow\dfrac{x+7}{x^2-4}\ge0\Rightarrow\left[{}\begin{matrix}-7\le x< -2\\x>2\end{matrix}\right.\)
\(\Rightarrow S\cap\left(-2;2\right)=\varnothing\)

a)11x-7<8x+7
<-->11x-8x<7+7
<-->3x<14
<--->x<14/3 mà x nguyên dương
---->x \(\in\){0;1;2;3;4}
b)x^2+2x+8/2-x^2-x+1>x^2-x+1/3-x+1/4
<-->6x^2+12x+48-2x^2+2x-2>4x^2-4x+4-3x-3(bo mau)
<--->6x^2+12x-2x^2+2x-4x^2+4x+3x>4-3+2-48
<--->21x>-45
--->x>-45/21=-15/7 mà x nguyên âm
----->x \(\in\){-1;-2}

Ta có: 5x – 2(4- x) >0
⇔ 5 x - 8 + 2 x > 0 ⇔ 7 x > 8 ⇔ x > 8 7
Tập nghiệm của bất phương trình đã cho là: S = 8 7 ; + ∞

a: Vì 2,99<3 nên 2,99 là nghiệm của bất phương trình 3>x
2,991; 2,992; 2,993
b: Vì 4,01>4 nên 4,01 là nghiệm của bất phương trình 4<x
4,004; 4,005; 4,006
a: Vì 2,99<3 nên 2,99 là nghiệm của bất phương trình 3>x
2,991; 2,992; 2,993
b: Vì 4,01>4 nên 4,01 là nghiệm của bất phương trình 4<x
4,004; 4,005; 4,006

đk: \(x\ne\pm6\)
Ta có: \(\frac{x^2-3x-5}{x^2-36}\ge1\)
\(\Leftrightarrow\frac{x^2-3x-5}{x^2-36}-1\ge0\)
\(\Leftrightarrow\frac{x^2-3x-5-x^2+36}{x^2-36}\ge0\)
\(\Leftrightarrow\frac{-3x+31}{x^2-36}\ge0\)
Xét 2 TH sau:
TH1: \(\hept{\begin{cases}-3x+31\ge0\\x^2-36>0\end{cases}}\) \(\Rightarrow x\le\frac{31}{3}\) và \(\orbr{\begin{cases}x>6\\x< -6\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}\frac{31}{3}\ge x>6\\x< -6\end{cases}}\)
TH2: \(\hept{\begin{cases}-3x+31\le0\\x^2-36< 0\end{cases}}\Leftrightarrow\hept{\begin{cases}x\ge\frac{31}{3}\\-6< x< 6\end{cases}}\) => Vô lý
Vậy tập nghiệm phương trình \(\orbr{\begin{cases}\frac{31}{3}\ge x>6\\x< -6\end{cases}}\)