Cho hình hộp chữ nhật ABCD.A'B'C'D', biết AB = 2AD và tổng diện tích 6 mặt bằng 12, thì hình hộp có thể tích lớn nhất ( V m a x ) bằng bao nhiêu?
A. V m a x = 8 3
B. V m a x = 2 2
C. V m a x = 3
D. V m a x = 10 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Thể tích khối cầu ngoại tiếp tứ diện ABCD’ chính là thể tích khối cầu ngoại tiếp hình hộp chữ nhật ABCD.A’B’C’D’. Khi đó, bán kính khối cầu ngoại tiếp là R = A C ' 2 .
Ta có V = 4 3 πR 3 = 4 3 π . AC ' 3 8 = 9 2 πa 3 ⇒ AC ' 3 = 27 a 3 ⇒ AC ' = 3 a .
Mặt khác A C ' 2 = A B 2 + A D 2 + A A ' 2 ⇒ A D 2 = ( 3 a 2 ) - a 2 - ( 2 a ) 2 = 4 a 2 ⇒ A D = 2 a .
Vậy thể tích của hình hộp chữ nhật ABCD.A'B'C'D' là V = A A ' . A B . A D = a . 2 a . 2 a = 4 a 3 .

Phương pháp:
Công thức tính thể tích khối hộp chữ nhật ABCD.A'B'C'D' là V = AA'.AB.AD
Cách giải:
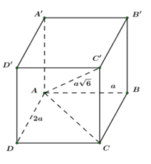
Ta có: ![]() (định lý Pitago)
(định lý Pitago)
Xét tam giác ACC’ vuông tại C ta có:
![]()
![]()
![]()
Chọn C.

Đáp án B
Giả độ dài các cạnh của khối hộp lần lượt là a; b; c khi đó T = 2ab + 2bc + 2ca = 36.
⇔ a b + b c + c a = 18 . Mặt khác A C ' = A B 2 + A D 2 + A A ' 2 = a 2 + b 2 + c 2 = 6
Khi đó a 2 + b 2 + c 2 = 36 a b + b c + c a = 18 ⇒ a + b + c 2 = 72 a b + b c + c a = 18 ⇔ a + b + c = 6 2 b a + c + a c = 18
Ta có: V = a b c = b . 18 - b a + c = b 18 - b 6 2 - b = b 3 - 6 2 b 2 + 18 b = f b
Xét f b = b 3 - 6 2 b 2 + 18 b , 0 < b < 6 2 ta có : f ' b = 3 b 2 - 12 2 b + 18 = 0 ⇔ b 2 - 4 b 2 + 6 = 0
⇔ [ b = 3 2 b = 3 ⇒ f 3 2 = 0 ; f 2 = 8 2 ⇒ M a x ( 0 ; 6 2 ) f b = 8 2 .

Chọn C
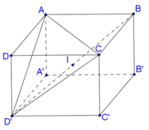
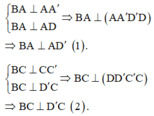
Từ (1), (2) dễ dàng suy ra trung điểm I của
BD' là tâm mặt cầu ngoại tiếp tứ diện ABCD'
Ta có

Đáp án A