Cho hình lập phương ABCD A'B'C'D' có cạnh bằng a. Tính theo a khoảng cách giữa hai đường thẳng AB' và BC'.
A. a 3 3
B. a 2 3
C. a 3 2
D. a 2 2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
24 tháng 8 2019
Đáp án D.
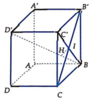
Cách 1: Gọi I là giao điểm của BC' và B'C . Trong B C ' D ' kẻ I H ⊥ B D ' tại H.
Ta có
B C ' ⊥ B ' C D ' C ' ⊥ B ' C B C ' , D ' C ' ∈ B C ' D ' ⇒ B ' C ⊥ B C ' D ' ⇒ B ' C ⊥ I H
Suy ra IH là đường vuông góc chung của BD' và B ' C ⇒ d B D ' , B ' C = I H .
Hai tam giác vuông BC'D' và BHI đồng dạng
⇒ I H D ' C ' = B I B D ' = a 2 2 a 3 = 6 6 ⇒ I H = a 6 6
Ta chọn D.
Cách 2: (Tọa độ hóa . Độc giả tự thực hiện)
HQ
Hà Quang Minh
Giáo viên
22 tháng 9 2023
a) \(AA'C'C\) là hình chữ nhật
\(\left. \begin{array}{l} \Rightarrow AC\parallel A'C'\\A'C' \subset \left( {A'C'B} \right)\end{array} \right\} \Rightarrow AC\parallel \left( {A'C'B} \right)\)
\(ABC'D'\) là hình bình hành
\(\left. \begin{array}{l} \Rightarrow AD'\parallel BC'\\BC' \subset \left( {A'C'B} \right)\end{array} \right\} \Rightarrow AD'\parallel \left( {A'C'B} \right)\)
Ta có:
\(\left. \begin{array}{l}AC\parallel \left( {A'C'B} \right)\\AD'\parallel \left( {A'C'B} \right)\\AC,A{\rm{D}}' \subset \left( {AC{\rm{D}}'} \right)\end{array} \right\} \Rightarrow \left( {AC{\rm{D}}'} \right)\parallel \left( {A'C'B} \right) \Rightarrow \left( {\left( {AC{\rm{D}}'} \right),\left( {A'C'B} \right)} \right) = {0^ \circ }\)
b) Ta có:
\(\left. \begin{array}{l}AB\parallel A'B'\\A'B' \subset \left( {A'B'C'D'} \right)\end{array} \right\} \Rightarrow AB\parallel \left( {A'B'C'D'} \right) \Rightarrow \left( {AB,\left( {A'B'C'D'} \right)} \right) = {0^ \circ }\)
CM
16 tháng 12 2017
Đáp án D
Gọi I là giao điểm của AC và BD
A I ⊥ B D A I ⊥ B B ' ⇒ A I ⊥ B B ' D ' D
=> B’I là hình chiếu vuông góc của AB’ lên (BB’D’D)
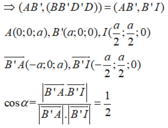
Đáp án A.
Đặt B ' 0 ; 0 ; 0 , A ' a ; 0 ; 0 , C ' 0 ; a ; 0 , B 0 ; 0 ; a ⇒ A a ; 0 ; a
Ta có B ' A → = a ; 0 ; a , B C ' → = 0 ; a ; − a , B ' B → = 0 ; 0 ; a
⇒ B ' A → , B C ' → = − a 2 ; a 2 ; a 2 ; B ' A → , B C ' → . B B ' → = a 3
d B ' A , B C ' = B ' A → , B C ' → . B B ' → B ' A → , B C ' → = a 3 3 a 4 = a 3 a 2 3 = a 3 3