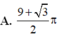
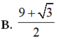
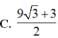
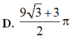
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Gọi S(x) là diện tích thiết diện đã cho thì S x = 2 sin x 2 . 3 4 = 3 sin x
Thể tích vật thể là V = ∫ 0 π S x d x = ∫ 0 π 3 sin x d x = 2 3
Đáp án C
Cạnh của thiết diện là a = 4 x + x diện tích thiết diện
S = 3 4 a 2 = 3 4 4 x + x
Vậy thể tích của hình cần tính là:
V = ∫ 0 3 3 4 4 x + x = 9 3 + 3 2
Đáp án cần chọn là C
Chọn B
Nếu S(x) là diện tích thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox thì thể tích của vật thể giới hạn bởi hai mặt phẳng x = a và x = b là
V = ∫ a b S x d x
Đáp án C
Do thiết diện là một tam giác đều nên diện tích thiết diện là:
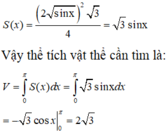
Chọn B
Nếu S(x) là diện tích thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox thì thể tích của vật thể giới hạn bửi hai mặt phẳng x = a và x = b là
Đáp án D
Diện tích tam giác bằng 2 sin x 2 3 4 = 3 sin x .
Suy ra thể tích cần tích bằng V = ∫ 0 π 3 sin x d x = - 3 cos x 0 π = 2 3 .
Đáp án C