Trong không gian với hệ tọa độ Oxyz, cho ba điểm M(2;2;1), N - 8 3 ; 4 3 ; 8 3 , E(2;1;-1). Đường thẳng ∆ đi qua tâm đường tròn nội tiếp của tam giác OMN và vuông góc với mặt phẳng (OMN). Khoảng cách từ điểm E đến đường thẳng ∆ là
A. 2 17 3
B. 3 17 5
C. 3 17 2
D. 5 17 3





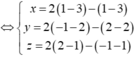
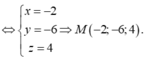

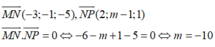


Đáp án A
Phương pháp giải:
Tìm tọa độ tâm đường tròn ngoại tiếp tam giác OMN bằng tính chất đường phân giác
Vectơ chỉ phương của
Kẻ phân giác OF (F ∈ MN) ta có:
Gọi I là tâm đường tròn nội tiếp tam giác OMN
Tam giác OMN vuông tại O, có bán kính đường tròn nội tiếp r=2 => OI = 2
Phương trình đường thẳng ∆ là
đi qua I(0;1;1)
Khoảng cách từ E đến đường thẳng ∆ là