Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B
Gọi I là tâm đường tròn nội tiếp tam giác OMN.
Ta áp dụng tính chất sau: “Cho tam giác OMN với I là tâm đường tròn nội tiếp, ta có ![]() với a = MN, b = ON, c = OM”.
với a = MN, b = ON, c = OM”.
Ta có:

![]()

Mặt phẳng (Oxz) có phương trình y = 0.
Mặt cầu tiếp xúc với mặt phẳng (Oxz) nên mặt cầu có bán kính R = d (I, (Oxz)) = 1.
Vậy phương trình mặt cầu là x²+ (y-1)²+ (z-1)²=1.

Chọn A
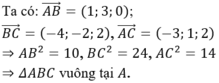
Tâm I của đường tròn ngoại tiếp tam giác là trung điểm của BC => I (0; 2; 0)
Đường thẳng d cần tìm đi qua I (0; 2; 0) và nhận vectơ ![]() làm véc tơ chỉ phương. Phương trình chính tắc của đường thẳng d là
làm véc tơ chỉ phương. Phương trình chính tắc của đường thẳng d là ![]()

Chọn D
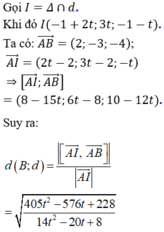
Xét hàm số:
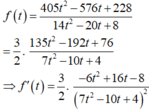
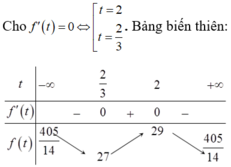
Do đó d (B; d) nhỏ nhất khi f(t) đạt giá trị nhỏ nhất bằng 27 tại t = 2/3. Suy ra ![]() . Chọn một vectơ chỉ phương của đường thẳng d là
. Chọn một vectơ chỉ phương của đường thẳng d là ![]()
Vậy phương trình đường thẳng ![]()

Đáp án B.
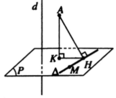
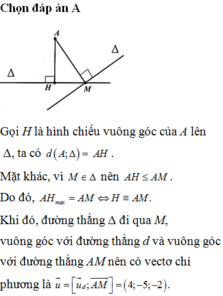
Gọi (P) là mặt phẳng qua M và vuông góc với d.Phương trình của ![]()
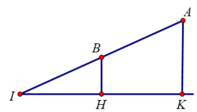
Gọi H,K lần lượt là hình chiếu vuông góc cùa A trên ∆,(P)
Ta có: K(-3;-2;-1), ![]()
Vậy khoảng cách từ A đến bé nhất khi A đi qua M,K.
∆ có vectơ chỉ phương ![]()

Chọn A
Cách 1:
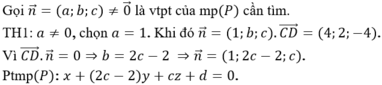

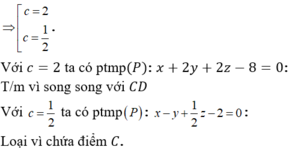

Cách 2: Ta có 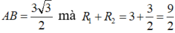 nên hai mặt cầu cắt nhau theo một đường tròn giao tuyến.
nên hai mặt cầu cắt nhau theo một đường tròn giao tuyến.
Gọi I = AB ∩ (α) với (α) là mặt phẳng thỏa mãn bài toán.
Hạ vuông góc với mặt phẳng .
Khi đó ta có I nằm ngoài AB và B là trung điểm AI vì
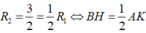
Suy ra I (2;1;2). Gọi (α): a(x-2) + b(y-1) + c(z-2) = 0.
Vì (α) // CD mà ![]() nên ta có 2a + b - 2c = 0 => b = 2c - 2a
nên ta có 2a + b - 2c = 0 => b = 2c - 2a
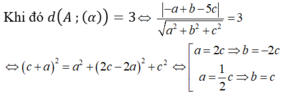
Ta có hai trường hợp:
Nếu b = -2c; a = 2c => (α): 2c (x-2) + 2c (y-1) + c(z-2) = 0 => 2x - 2y + z - 4 = 0
Mặt khác CD // (α) nên CD ∉ (α) loại trường hợp trên.
Nếu b = c; a = c/2 => (α): c/2 . (x-2) + c (y-1) + c(z-2) = 0 => x + 2y + 2z - 8 = 0
Kiểm tra thấy CD ∉ (α) nên nhận trường hợp này. Vậy (α): x + 2y + 2z - 8 = 0
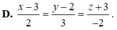

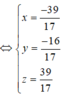

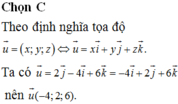
Đáp án A
Phương pháp giải:
Tìm tọa độ tâm đường tròn ngoại tiếp tam giác OMN bằng tính chất đường phân giác
Vectơ chỉ phương của
Kẻ phân giác OF (F ∈ MN) ta có:
Gọi I là tâm đường tròn nội tiếp tam giác OMN
Tam giác OMN vuông tại O, có bán kính đường tròn nội tiếp r=2 => OI = 2
Phương trình đường thẳng ∆ là
đi qua I(0;1;1)
Khoảng cách từ E đến đường thẳng ∆ là