Trên mặt nước có hai nguồn phát sóng dao động cùng tần số và vuông pha với nhau trên phương vuông góc với mặt chất lỏng và gây ra hiện tượng giao thoa. Nhận xét nào dưới đây là đúng ?
A. Tổng số vân cực đại giao thoa là một số lẻ
B. Đường trung trực của đoạn thẳng nối hai nguồn trên mặt nước là một vân cực đại
C. Tổng số vân cực đại bằng tổng số vân cực tiểu
D. Tổng số vân cực tiểu giao thoa là một số lẻ

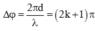
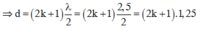
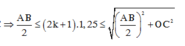
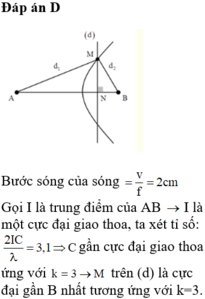
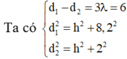

Đáp án C
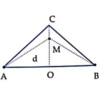
Do hai nguồn dao động vuông pha nên hệ vân cực đại đối xứng với hệ vân cực tiểu qua đường trung trực của đoạn thẳng nối hai nguồn → Tổng số vân cực đại bằng tổng số vân cực tiểu.