Trong không gian với hệ tọa độ Oxyz, biết rằng tập hợp các điểm M x ; y ; z sao cho x + y + z = 3 là một hình đa diện. Tính thể tích V của khối đa diện đó
A. V = 54
B. V = 72
C. V = 36
D. V = 27
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Gọi M x ; y ; z ⇒ A M → = x − 1 ; y ; z + 3 , B M → = x + 3 ; y + 2 ; z + 5
Khi đó A M 2 + B M 2 = 30 ⇔ x − 1 2 + y 2 + z + 3 2 + x + 3 2 + y + 2 2 + z + 5 2 = 30
⇔ x − 1 2 + y + 1 2 + z + 4 2 = 9 ⇒ M ∈ S có tâm I − 1 ; − 1 ; − 4 , R = 3

Chọn C
Gọi tọa độ điểm M(x;y;z)
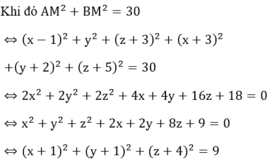
là phương trình của mặt cầu (S), có tâm I (-1;-1;-4) và bán kính R = 3

Đáp án C
![]()
là trung điểm của AB khi đó M A 2 + M B 2 = 30
Suy ra
![]()
![]()
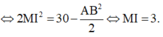
Do đó mặt cầu (S) tâm I(-1;-1;-4), R =3

Chọn B.
Phương pháp:
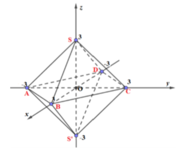
Hình đa diện được lập thành là hình bát diện đều.
Cách giải:

Đáp án C.
Ta có x + y + z = 3 ⇔ x 3 + y 3 + z 3 = 1 . Suy ra tập hợp các điểm M x ; y ; z là 8 mặt chắn có phương trình: ;
x 3 + y 3 + z 3 = 1 ; x − 1 + y − 3 + z − 3 = 1 ; x − 3 + y − 3 + z 3 = 1
x − 3 + y 3 + z − 3 = 1 ; x 3 + y − 3 + z − 3 = 1 ; x − 3 + y 3 + z 3 = 1 ; x 3 + y − 3 + z 3 = 1 ; x 3 + y 3 + z − 3 = 1
Các mặt chắn này cắt các trục Ox, Oy, Oz tại các điểm , A − 3 ; 0 ; 0 , B 3 ; 0 ; 0 , C 0 ; − 3 ; 0 D 0 ; 3 ; 0 , E 0 ; 0 ; − 3 , F 0 ; 0 ; 3 .
Từ đó, tập hợp các điểm M x ; y ; z thỏa mãn x + y + z = 3 là các mặt bên của bát diện đều x + y + z = 3 (hình vẽ) cạnh bằng 3 2 .
Thể tích khối bát diện đều là V = 3 2 3 . 2 3 = 36 (đvtt).