Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án là A.
+ Mặt phẳng chứa Ox có dạng B y + C z = 0
+ Do mặt cầu tiếp xúc với mặt phẳng nên:
2 B − C B 2 + C 2 = 1 ⇔ B = 0 B = 4 , C = 3
Vậy mặt phẳng cần tìm 4 y + 3 z = 0
Đáp án là A.
+ Mặt phẳng chứa Ox có dạng By+Cz=0
+ Do mặt cầu tiếp xúc với mặt phẳng nên 2 B - C B 2 + C 2 = 1 ⇔ B = 0 B = 4 , C = 3
Vậy mặt phẳng cần tìm 4y +3z=0
Chọn A
Mặt cầu (S) có tâm I (1; 2; -1) và bán kính R = 1
Gọi vectơ pháp tuyến của mặt phẳng (Q) là 
với
Mặt khác (Q) chứa trục hoành nên (Q) có phương trình dạng (Q): By + Cz = 0
Lại có (Q) tiếp xúc mặt cầu (S) nên
+ Với B = 0 thì phương trình mặt cầu là z = 0 ( chính là mặt phẳng 0xy)
+ Với 3B – 4C = 0, chọn B = 4 => C = 3. Vậy (Q): 4y + 3z = 0
Đáp án B
Pt pháp tuyến của mặt phẳng cần tìm là n ⇀ = d , ⇀ ∆ ⇀ = (1;0;1)
Pt có dạng: x+z+D=0
Khoảng cách từ O (-1;1;-2) đến mp là 2
⇒ D=1
Pt có dạng : x+z+1=0
Chọn D
Gọi vectơ pháp tuyến của mặt phẳng (P) là 
, a²+b²+c²>0.
Phương trình mặt phẳng (P): a(x-4)+b (y-3)+c (z-4)=0.
Do (P) // Δ nên -3a+2b+2c=0 => 3a = 2 (b + c)
Mặt phẳng (P) tiếp xúc với (S) nên
Thay 3a=2 (c+b ) vào (*) ta được:
TH1: 2b-c=0, chọn b=1; c=2 => a = 2 => (P): 2x+y+2z-19=0 (thỏa).
TH2: b-2c=0, chọn c=1; b=2 => a = 2 => (P): 2x+2y+z-18=0 (loại do Δ ⊂ (P))
Đáp án A
Do (P) tiếp xúc với (S) nên bán kính của (S) là R = d(I, (P)) = 
= 3. Vậy phương trình mặt cầu (S) là (x-1)² + y² + (z+2)² =9.
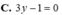
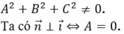
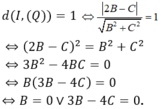
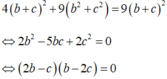
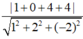
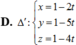
Đáp án D.
Mặt cầu (S) có tâm I 1 ; − 2 ; 3 và bán kính R=5 . Mặt phẳng Q / / P nên (Q) có phương trình là 2 x + 2 y − z + m = 0, m ≠ 17 .
Mặt phẳng (Q) cắt mặt cầu (S) theo giao tuyến là đường tròn có bán kính r, chu vi bằng 6 π nên 2 π r = 6 π ⇔ r = 3 .
Khoảng cách từ I đến mặt phẳng (Q) là d I ; Q = R 2 − r 2 = 5 2 − 3 2 = 4 .
Khi đó
2.1 + 2. − 2 − 3 + m 2 2 + 2 2 + − 1 2 = 4 ⇔ m − 5 = 12 ⇔ m − 5 = 12 m − 5 = − 12 ⇔ m = 17 L m = − 7 t m
Vậy phương trình mặt phẳng (Q) là 2 x + 2 y − z − 7 = 0