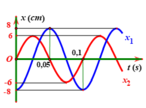
Cho hai dao động điều hòa với li độ x 1 và x 2 có đồ thị như hình vẽ. Tổng tốc độ của hai dao động ở cùng một thời điểm có giá trị lớn nhất là
A. 200π cm/s
B. 140π cm/s
C. 280π cm/s
D. 2100π cm/s
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Chọn B
+ Từ đồ thị ta có: hai dao động đều có T = 0,1s => ω = 20π rad/s.
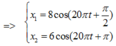
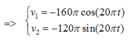
+ Gỉa sử trong thời điểm t, tổng tốc độ của hai dao động có giá trị lớn nhất.
Áp dụng bất đẳng thức Bunhiacopxki:
![]()
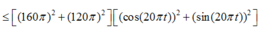
![]()
![]()

Chọn C
+Chu kỳ dao động T = 0 , 1 s . Tần số góc ω = 20 π r a d / s
Phương trình dao động của hai vật: x 1 = 8 cos 20 π t − π 2 c m x 2 = 6 cos 20 π t − π c m
Hai dao động vuông pha nhau nên vận tốc của vật cũng vuông pha nhau:
v 1 = 160 π cos 20 π t − π 2 c m / s v 2 = 120 π cos 2 π t − π c m / s
Khi đó: v = v 1 + v 2 = 200 π cos 20 π t + α c m / s .
Suy ra: v max = 200 π c m / s

Giải thích: Đáp án D
+ Từ đồ thị ta có: 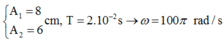 và hai dao động vuông pha
và hai dao động vuông pha
→Tổng vận tốc tức thời cực đại: ![]()

Chọn đáp án B
+ Dựa vào đồ thị ta viết được phương trình li độ của hai chất điểm
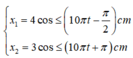
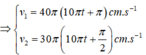
![]()
![]()
![]()
![]()