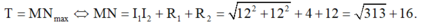Cho hai số phức z 1 , z 2 thỏa mãn z 1 - 3 i + 5 = 2 và i z 2 - 1 + 2 i = 4 .
Tìm giá trị lớn nhất của biểu thức T = 2 i z 1 + 3 z 2
A. 313 + 16
B. 313
C. 313 + 8
D. 313 + 2 5
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Phương pháp: Cho z1, z2 là hai số phức bất kì, khi đó | z1.z2 | = |z1|.|z2|
Cách giải: Ta có:
![]()
![]()

\(z=x+yi\Rightarrow\left(x+1\right)^2+\left(y+1\right)^2=x^2+y^2\)
\(\Rightarrow x+y+1=0\Rightarrow\) tập hợp z là đường thẳng d: \(x+y+1=0\)
\(P=\left|\left(z-4-5i\right)-\left(w-3-4i\right)\right|\ge\left|\left|z-4-5i\right|-\left|w-3-4i\right|\right|=\left|\left|z-4-5i\right|-1\right|\)
Gọi M là điểm biểu diễn z và \(A\left(4;5\right)\Rightarrow\left|z-4-5i\right|=AM\)
\(AM_{min}=d\left(A;d\right)=\dfrac{\left|4+5+1\right|}{\sqrt{1^2+1^2}}=5\sqrt{2}\)
\(\Rightarrow P\ge\left|5\sqrt{2}-1\right|=5\sqrt{2}-1\)

Chọn C.
Đặt z = a+ bi.
Theo đề ra ta có: ( 3 + i) z = 2
Hay ( 3 + i)( a + bi) = 2
Suy ra: 3a - b + ( 3b + a) i = 2
![]()
nên z = 3/5 - 1/5i.
Khi đó w = 3/5 - 1/5i + 2/5 - 4/5 i = 1 - i.
Vậy ![]()
Đáp án A.
Phương pháp giải:
Đưa về biện luận vị trí giữa hai điểm thuộc đường tròn để khoảng cách của chúng lớn nhất
Lời giải:
Ta có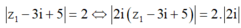
Và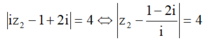
Đặt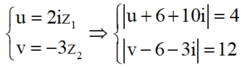
và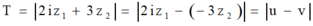
Tập hợp điểm M biểu diễn số phức u là đường tròn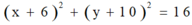 tâm
I
1
(
-
6
;
-
10
)
,
R
1
=
4
tâm
I
1
(
-
6
;
-
10
)
,
R
1
=
4
Tập hợp điểm N biểu diễn số phức v là đường tròn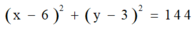 tâm
I
2
(
6
;
3
)
,
R
2
=
4
tâm
I
2
(
6
;
3
)
,
R
2
=
4
Khi đó