Cho hàm số f ( x ) = ( 1 - x + x 2 ) 10 Giá trị đạo hàm cấp 5 của hàm số tại x o = 1 là
A. 34848
B. 30240
C. 125240
D. 174240
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáp án A
Phương pháp:
Dựa vào khái niệm cực trị và các kiến thức liên quan.
Cách giải:
(1) chỉ là điều kiện cần mà không là điều kiện đủ.
VD hàm số y = x3 có y' = 3x2 = 0 ⇔ x = 0. Tuy nhiên x = 0 không là điểm cực trị của hàm số.
(2) sai, khi f''(x0) = 0, ta không có kết luận về điểm x0 có là cực trị của hàm số hay không.
(3) hiển nhiên sai.
Vậy (1), (2), (3): sai; (4): đúng

- Ta có:
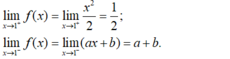
- Hàm số đã cho có đạo hàm tại x = 1 nên hàm số liên tục tại x = 1.
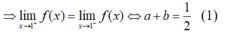
- Hàm số có đạo hàm tại x = 1 nên giới hạn 2 bên của 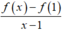 bằng nhau, ta có:
bằng nhau, ta có:
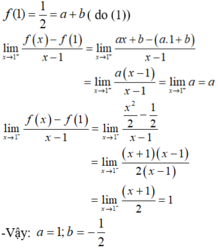
Chọn A.

Trước hết ta xét: \(g\left(x\right)=\dfrac{1}{x+a}=\left(x+a\right)^{-1}\) với a là hằng số bất kì
\(g'\left(x\right)=-1.\left(x+a\right)^{-2}=\left(-1\right)^1.1!.\left(x+a\right)^{-\left(1+1\right)}\)
\(g''\left(x\right)=-1.\left(-2\right).\left(x+a\right)^{-3}=\left(-1\right)^2.2!.\left(x+a\right)^{-\left(2+1\right)}\)
Từ đó ta dễ dàng tổng quát được:
\(g^{\left(n\right)}\left(x\right)=\left(-1\right)^n.n!.\left(x+a\right)^{-\left(n+1\right)}=\dfrac{\left(-1\right)^n.n!}{\left(x+a\right)^{n+1}}\)
Xét: \(f\left(x\right)=\dfrac{x^2+1}{x\left(x-2\right)\left(x+2\right)}=-\dfrac{1}{4}.\left(\dfrac{1}{x}\right)+\dfrac{5}{8}\left(\dfrac{1}{x+2}\right)+\dfrac{5}{8}\left(\dfrac{1}{x-2}\right)\)
Áp dụng công thức trên ta được:
\(f^{\left(30\right)}\left(1\right)=\dfrac{1}{4}.\dfrac{\left(-1\right)^{30}.30!}{1^{31}}+\dfrac{5}{8}.\dfrac{\left(-1\right)^{30}.30!}{\left(1+2\right)^{31}}+\dfrac{5}{8}.\dfrac{\left(-1\right)^{30}.30!}{\left(1-2\right)^{31}}\)
Bạn tự rút gọn kết quả nhé
\(f\left(x\right)=\dfrac{x^2+1}{x^3}-4x\) hay \(f\left(x\right)=\dfrac{x^2+1}{x^3-4x}\) bạn?

B
Từ đồ thị của hàm số f"(x) ta có bảng biến
thiên của hàm số f'(x) như sau:
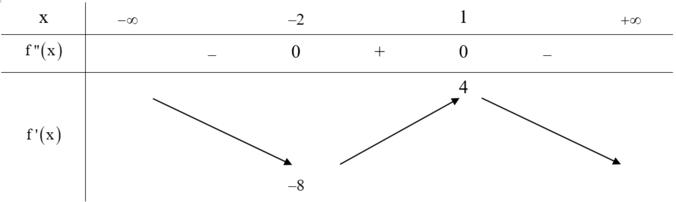

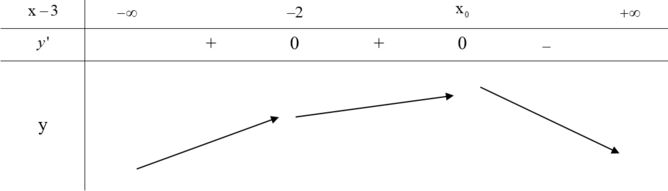
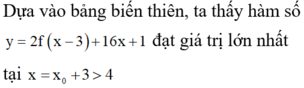

Đáp án A
Hàm số f(x) xác định trên D⊆ R
Điểm
x
0
∈ D được gọi là điểm cực đại của hàm số f(x) nếu tồn tại một khoảng (a;b)⊂ D sao cho
x
0
∈ (a;b) và f(
x
0
)>f(x),∀x ∈ (a,b)∖{
x
0
}.