Biết rằng phương trình x - 2 log 2 4 x - 2 = 4 . x - 2 3 có hai nghiệm x1, x2 (x1 < x2). Tính 2x1 – x2.
A. 1.
B. 3.
C. -5.
D. -1.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D.
ĐK: x > 2.
TH1: Ta thấy x = 3 không phải là nghiệm của PT.
TH2: Với x ≠ 3 logarit cơ số x - 2 cả 2 vế ta được log 2 4 x - 2 = log x - 2 4 + 3
⇔ 2 + log 2 x - 2 = 2 log x - 2 2 + 3 ⇔ log 2 x - 2 - 2 log x - 2 2 - 1 = 0
Đặt t = log 2 x - 2 ⇒ t - 2 t - 1 = 0 ⇔ t 2 - t - 2 = 0 ⇔ [ t = - 1 t = 2
Với t = - 1 ⇒ x = 5 2 ; với t = 2 ⇒ x = 6 ⇒ [ x 1 = 5 2 x 2 = 6 ⇒ 2 x 1 - x 2 = - 1 .

Chọn A.
ĐK: x > 2
Pt ⇔ log3(x – 2)2(x – 4)2 = 0
⇔ (x – 2)2(x – 4)2 = 1
Với 2 < x< 4 suy ra (x - 2)(4 - x) = 1 ⇔ x = 3 (tm)
Với x ≥ 4 suy ra (x - 2)(x - 4) = 1 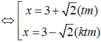
Suy ra (x1 – x2)2 = (3 – 3 – √2)2 = 2

\(ĐK:x>2\\ Pt\Leftrightarrow\log_3\left(x-2\right)^2\left(x-4\right)^2=0\\ \Leftrightarrow\left(x-2\right)^2\left(x-4\right)^2=1\Leftrightarrow\left[{}\begin{matrix}x^2-6x+9=0\\x^2-6x+7=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\3+\sqrt{2}\end{matrix}\right.\)
\(\left(x_1-x_2\right)^2=\left(\sqrt{2}+3-3\right)^2=2\)

Hai số 1 - 2 và 1 + 2 là nghiệm của phương trình :
[x – (1 - 2 )][x – (1 + 2 )] = 0
⇔ x 2 – (1 + 2 )x – (1 - 2 )x + (1 - 2 )(1 + 2 ) = 0
⇔ x 2 – 2x – 1 = 0

a: Δ=(m+1)^2-4m=(m-1)^2>=0
=>Phương trình luôn có nghiệm
b: x1^2+x2^2+3x1x2=5
=>(x1+x2)^2+x1x2=5
=>(m+1)^2+m=5
=>m^2+3m-4=0
=>(m+4)(m-1)=0
=>m=1 hoặc m=-4

Hai số 2 và 5 là nghiệm của phương trình :
(x – 2)(x – 5) = 0 ⇔ x 2 – 7x + 10 = 0

Hai số -1/2 và 3 là nghiệm của phương trình :
(x + 1/2 )(x – 3) = 0 ⇔ 2 x 2 – 5x – 3 = 0

Hai số 0,1 và 0,2 là nghiệm của phương trình :
(x – 0,1)(x – 0,2) = 0 ⇔ x 2 – 0,3x + 0,02 = 0
Đáp án D.
ĐK: x > 2.
TH1: Ta thấy x = 3 không phải là nghiệm của PT.
TH2: Với x ≠ 3 logarit cơ số x – 2 cả 2 vế ta được