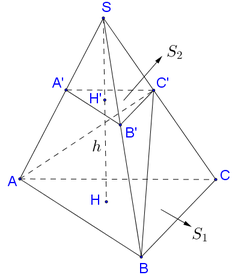
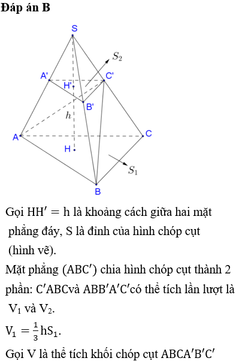
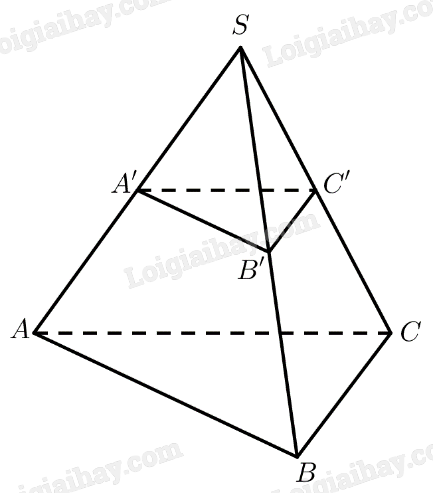
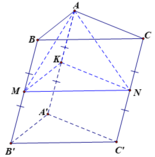
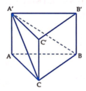
Cho khối chóp cụt ABC A'B'C' với hai đáy ABC và A'B'C' có diện tích lần lượt bằng 4 và 9. Mặt phẳng (ABC') chia khối chóp cụt thành hai phần. Gọi H 1 là phần chứa đỉnh C và H 2 là phần còn lại. Tính tỉ số thể tích H 1 và H 2 .
A. 2 5
B. 3 5
C. 9 10
D. 4 15

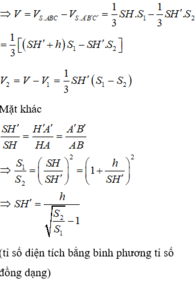
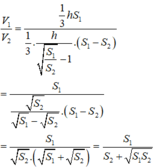

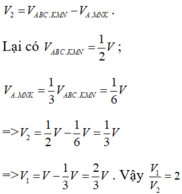


Đáp án D.
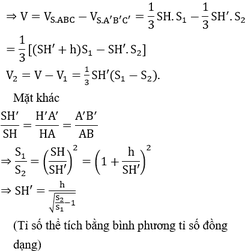
Thể tích khối chóp cụt A B C . A ' B ' C ' được tính bằng công thức
V = h 3 B + B ' + B B ' = h 3 + 4 + 9 + 4.9 = 19 3 h
Thể tích của phần được tính bằng công thức V 1 = 1 3 . h .4 = 4 3 h
Tỉ số thể tích giữa ( H 1 ) và ( H 2 ) là 4 3 h 19 3 h − 4 3 h = 4 15 . Ta chọn D.