a) x(x2 +4x +5) – x2(x +4)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
15 tháng 8 2024
A = - 3\(x\).(\(x-5\)) + 3(\(x^2\) - 4\(x\)) - 3\(x\) - 10
A = - 3\(x^2\) + 15\(x\) + 3\(x^2\) - 12\(x\) - 3\(x\) - 10
A = (- 3\(x^2\) + 3\(x^2\)) + (15\(x\) - 12\(x\) - 3\(x\)) - 10
A = 0 + (3\(x-3x\)) - 10
A = 0 - 10
A = - 10
18 tháng 10 2021
\(A=x^2+4x-21-x^2-4x+5=-16\\ B=-2\left(4x^2+20x+25\right)-\left(1-16x^2\right)\\ B=-8x^2-40x-50-1+16x^2=8x^2-40x-51\\ C=x^2\left(x^2-16\right)-\left(x^4-1\right)=x^4-16x^2-x^4+1=1-16x^2\\ D=x^3+1-\left(x^3-1\right)=2\\ E=x^3-3x^2+3x-1-x^3+1-9x^2+1=-12x^2+3x+1\)
CM
25 tháng 8 2019
a) x = -1. b) x = 4 hoặc x = 5.
c) x = ± 2 . d) x = 1 hoặc x = 2.
2 tháng 11 2021
\(a,\Rightarrow\left(2x-5\right)^2+2\left(2x-5\right)\left(x+2\right)+\left(x+2\right)^2=0\\ \Rightarrow\left(2x-5+x+2\right)^2=0\\ \Rightarrow3x-3=0\\ \Rightarrow x=1\\ b,\Rightarrow9-\left(x^2-5x\right)^2=9\\ \Rightarrow x^2-5x=0\\ \Rightarrow x\left(x-5\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\x=5\end{matrix}\right.\)
27 tháng 4 2023
`@` `\text {dnammv}`
`a,`
`4x(x^2-x-1)-(x^2-2)(x+3)`
`= 4x^3-4x^2-4x- [x^2(x+3)-2(x+3)]`
`= 4x^3-4x^2-4x- (x^3+3x^2-2x-6)`
`= 4x^3-4x^2-4x-x^3-3x^2+2x+6`
`= 3x^3 - 7x^2-2x+6`
`b,`
`(x+5)(x+7)-7x(x+3)`
`= x(x+7)+5(x+7)-7x^2-21x`
`= x^2+7+5x+35-7x^2-21x`
`= -6x^2-16x+35`
`c,`
`x(x^2-x-2)-(x+5)(x-1)`
`= x^3-x^2-2x- [x(x-1)+5(x-1)]`
`= x^3-x^2-2x- (x^2-x+5x-5)`
`= x^3-x^2-2x - x^2 + x -5x+5`
`= x^3-2x^2- 4x+5`
`d,`
`(x+5)(x+7)-(x-4)(x+3)`
`= x(x+7)+5(x+7)- [x(x+3)-4(x+3)]`
`= x^2+7x+5x+35 - (x^2+3x-4x-12)`
`= x^2+12x+35 - x^2+x+12`
`= 13x+47`
26 tháng 7 2021
1) \(\left(\dfrac{1}{2}x+3\right)\left(x^2-4x-6\right)\)
\(=\dfrac{1}{2}x^3-2x^2-3x+3x^2-12x-18\)
\(=\dfrac{1}{2}x^3+x^2-15x-18\)
2) \(\left(6x^2-9x+15\right)\left(\dfrac{2}{3}x+1\right)\)
\(=4x^3+6x^2-6x^2-9x+10x+15\)
\(=4x^3+x+15\)
3) Ta có: \(\left(3x^2-x+5\right)\left(x^3+5x-1\right)\)
\(=3x^5+15x^2-3x^2-x^4-5x^2+x+5x^3+25x-5\)
\(=3x^5-x^4+5x^3+10x^2+26x-5\)
4) Ta có: \(\left(x-1\right)\left(x+1\right)\left(x-2\right)\)
\(=\left(x^2-1\right)\left(x-2\right)\)
\(=x^3-2x^2-x+2\)
24 tháng 10 2023
Dễ
Thế
Mà
Cũnhoir
Dc
Ạ
Chịu
Chắc
Phải
Ngu
Lamqs
Mới
Hỏi
Câu
Này
DT
1
9 tháng 1 2022
\(a,4x^2-4y^2-20x+20y=4\left(x^2-y^2\right)-\left(20x-20y\right)=4\left(x-y\right)\left(x+y\right)-20\left(x-y\right)=\left(x-y\right)\left(4x+4y-20\right)=4\left(x-y\right)\left(x+y-5\right)\\ b,16x^2-25+\left(4x-5\right)=\left(4x-5\right)\left(4x+5\right)+\left(4x-5\right)=\left(4x-5\right)\left(4x+5+1\right)=\left(4x-5\right)\left(4x+6\right)=2\left(4x-5\right)\left(2x+3\right)\)
\(c,\left(x+5y\right)^3=x^3+15x^2y+75xy^2+125y^3\\ e,x^2-4x+4-y^2=\left(x-2\right)^2-y^2=\left(x-y-2\right)\left(x+y-2\right)\\ g,x^2-3x-4=\left(x^2-4x\right)+\left(x-4\right)=x\left(x-4\right)+\left(x-4\right)=\left(x+1\right)\left(x-4\right)\)
30 tháng 7 2021
1)(x2-4x+16)(x+4)-x(x+1)(x+2)+3x2=0
\(\Rightarrow\)(x3+64)-x(x2+2x+x+2)+3x2=0
\(\Rightarrow\)x3+64-x3-2x2-x2-2x+3x2=0
\(\Rightarrow\)-2x+64=0
\(\Rightarrow\)-2x=-64
\(\Rightarrow\)x=\(\dfrac{-64}{-2}\)
\(\Rightarrow x=32\)
30 tháng 7 2021
2)(8x+2)(1-3x)+(6x-1)(4x-10)=-50
\(\Rightarrow\)8x-24x2+2-6x+24x2-60x-4x+10=50
\(\Rightarrow\)-62x+12=50
\(\Rightarrow\)-62x=50-12
\(\Rightarrow\)-62x=38
\(\Rightarrow\)x=\(-\dfrac{38}{62}=-\dfrac{19}{31}\)
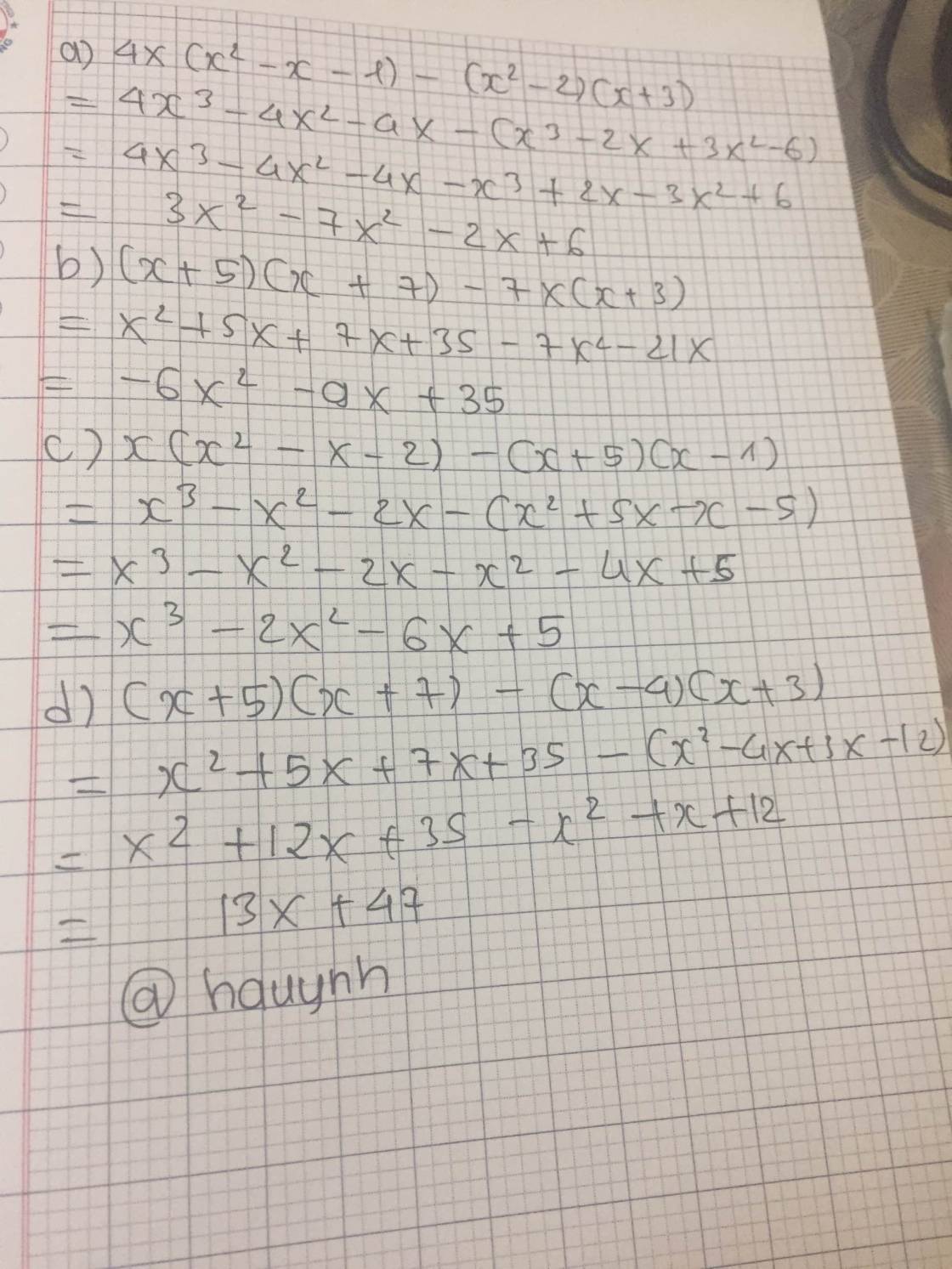
\(\Leftrightarrow x^3+4x^2+5x-x^3-4x^2=0\)
\(\Leftrightarrow5x=0\)
\(\Leftrightarrow x=0\)
vậy pt có tập nghiệm S={0}