Tìm giá trị x ∈ ℕ thỏa mãn C x 0 + C x x - 1 + C x x - 2 = 79
A. x =12
B. x =13
C. x =16
D. x =17
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

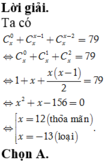

`a)|x-2|=2<=>[(x=4(ko t//m)),(x=0(t//m)):}`
Thay `x=0` vào `A` có: `A=[2\sqrt{0}-3]/[\sqrt{0}-2]=3/2`
`b)` Với `x >= 0,x ne 4` có:
`B=[2(\sqrt{x}-3)+\sqrt{x}(\sqrt{x}+3)-4\sqrt{x}]/[(\sqrt{x}+3)(\sqrt{x}-3)]`
`B=[2\sqrt{x}-6+x+3\sqrt{x}-4\sqrt{x}]/[(\sqrt{x}+3)(\sqrt{x}-3)]`
`B=[x+\sqrt{x}-6]/[(\sqrt{x}+3)(\sqrt{x}-3)]`
`B=[(\sqrt{x}+3)(\sqrt{x}-2)]/[(\sqrt{x}+3)(\sqrt{x}-3)]`
`B=[\sqrt{x}-2]/[\sqrt{x}-3]`
`c)` Với `x >= 0,x ne 4` có:
`C=A.B=[2\sqrt{x}-3]/[\sqrt{x}-2].[\sqrt{x}-2]/[\sqrt{x}-3]=[2\sqrt{x}-3]/[\sqrt{x}-3]`
Có: `C >= 1`
`<=>[2\sqrt{x}-3]/[\sqrt{x}-3] >= 1`
`<=>[2\sqrt{x}-3-\sqrt{x}+3]/[\sqrt{x}-3] >= 0`
`<=>[\sqrt{x}]/[\sqrt{x}-3] >= 0`
Vì `x >= 0=>\sqrt{x} >= 0`
`=>\sqrt{x}-3 > 0`
`<=>x > 9` (t/m đk)

b) Ta có:
\(\frac{a+b}{c}=\frac{b+c}{a}=\frac{c+a}{b}=\frac{a+b+b+c+c+a}{c+a+b}\) ( tính chất dãy tỉ số bằng nhau)
\(=\frac{2a+2b+2c}{a+b+c}=2\)
\(\Rightarrow\hept{\begin{cases}a+b=2c\\b+c=2a\\c+a=2b\end{cases}}\)
Ta có:
\(b+c=2a\)
\(\Rightarrow2b+2c=4a\)
Mà 2c=a+b
\(\Rightarrow\)2b+a+b=4a
\(\Rightarrow3b=3a\)
\(\Rightarrow a=b\)
Chứng minh tương tự:b=c;a=c
Thay vào biểu thức:
\(\left(1+\frac{a}{b}\right)\left(1+\frac{b}{c}\right)\left(1+\frac{c}{a}\right)=2\times2\times2=8\)8