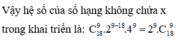Tìm số hạng không chứa x trong khai triển
x
2
+
2
x
6
với
x
≠
0
...
Đọc tiếp
Tìm số hạng không chứa x trong khai triển x 2 + 2 x 6 với x ≠ 0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
17 tháng 6 2018
Đúng(0)
Những câu hỏi liên quan
16 tháng 4 2023
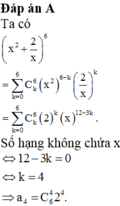
a: SHTQ là: \(C^k_{10}\cdot x^{10-k}\cdot\left(\dfrac{2}{x}\right)^k=C^k_{10}\cdot2^k\cdot x^{10-2k}\)
Số hạng ko chứa x tương ứng với 10-2k=0
=>k=5
=>SH đó là 8064
b: SHTQ là; \(C^k_6\cdot x^{6-k}\cdot\left(\dfrac{2}{x^2}\right)^k=C^k_6\cdot2^k\cdot x^{6-3k}\)
Số hạng ko chứa x tương ứng với 6-3k=0
=>k=2
=>Số hạng đó là 60
c: SHTQ là: \(C^k_5\cdot\left(3x^3\right)^{5-k}\cdot\left(-\dfrac{2}{x^2}\right)^k\)
\(=C^k_5\cdot3^{5-k}\cdot\left(-2\right)^k\cdot x^{15-5k}\)
SH chứa x^10 tương ứng với 15-5k=10
=>k=1
=>Hệ số là -810
CM
21 tháng 1 2019
Đáp án A
Ta có
x 2 + 2 x 6 = ∑ k = 0 6 C k 6 x 2 6 − k 2 x k = ∑ k = 0 6 C k 6 2 k x 12 − 3 k .
Số hạng không chứa x ⇔ 12 − 3 k = 0 ⇔ k = 4 ⇒ a 4 = C 6 4 2 4 .
CM
8 tháng 7 2019
Đáp án A
Ta có:
x 2 + 2 x 6 = ∑ k − 0 6 C 6 k x 2 6 − k 2 x k = ∑ k − 0 6 C 6 k 2 k x 12 − 3 k
Số hạng không chứa x = 12 − 3 k = 0
⇔ k = 4 ⇒ a 4 = C 6 4 2 4 .
CM
13 tháng 10 2019
Chọn C
Ta có: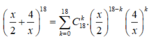 
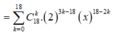
Số hạng tổng quát trong khai triển 
Số hạng không chứa x trong khai triển phải có: 
=> 18 - 2k = 0 => k = 9
Suy ra hệ số của số hạng không chứa x trong khai triển là: 
CM
14 tháng 3 2018
Chọn B.
Phương pháp:
Sử dụng công thức khai triển của nhị thức:
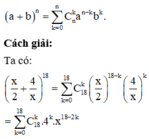
Số hạng không chứa x trong khai triển là số hạng thứ k với: 18 - 2k = 0
=> k = 9
