Xếp ngẫu nhiên 6 viên bi được ghi số từ 1 đến 6 thành một hàng ngang. Xác suất để tổng hai số ghi trên hai viên bi xếp cạnh nhau bất kì là một số tự nhiên có một chữ số bằng
A. 1 162
B. 2 5
C. 1 3
D. 3 20
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Tổng các viên bi lẻ khi số số viên bi lẻ là lẻ
Do đó ta có các trường hợp: trong 6 viên có (1 lẻ 5 chẵn), (3 lẻ 3 chẵn), (5 lẻ 1 chẵn)
Được chọn từ 6 viên lẻ (1;3;5;7;9;11) và 5 viên chẵn (2;4;6;8;10)
Không gian mẫu: \(n\left(\Omega\right)=C_{11}^6\)
Số cách chọn thỏa mãn: \(n\left(A\right)=C_6^1.C_5^5+C_6^3.C_5^3+C_6^5.C_5^1\)
Xác suất: \(P=\dfrac{n\left(A\right)}{n\left(\Omega\right)}=...\)

a) Việc xếp 9 viên bi sao cho không có hai viên bi trắng nào xếp liến nhau được thực hiện qua 2 công đoạn
Công đoạn 1: Xếp 4 viên bi xanh trước, vì các viên bi có kích thước khác nhau nên quan tâm đến thứ tự, suy ra công đoạn 1 có \(4! = 24\) cách
Công đoạn 2: Xếp 5 viên bi trắng vào 5 vị trí xung quanh bi xanh, có quan tâm đến thứ tự nên công đoạn 2 có \(5! = 120\) cách
Vậy có \(120.24 = 2880\) kết quả thuận lợi cho biến cố “Không có hai viên bi trắng nào xếp liền nhau”
b) Việc xếp 9 viên bi sao cho bốn viên bi xanh được xếp liền nhau được thực hiện qua 2 công đoạn
Công đoạn 1: Xếp 4 viên bi xanh liền nhau, vì các viên bi có kích thước khác nhau nên quan tâm đến thứ tự, suy ra công đoạn 1 có \(4! = 24\) cách
Công đoạn 2: Xếp 5 viên bi trắng có kích thước khác nhau vào bên trái hay bên phải của bi xanh, có quan tâm đến thứ tự nên công đoạn 2 có \(5!{.2^5} = 3840\) cách
Vậy có \(3840.24 = 92160\) kết quả thuận lợi cho biến cố “Bốn viên bi xanh được xếp liền nhau”

Không gian mẫu là số cách chọn ngẫu nhiên 3 viên bi từ hộp chứa 50 viên bi.
Suy ra số phần tử của không gian mẫu là ![]() .
.
Gọi A là biến cố “3 viên bi được chọn là một số chia hết cho 3 ’’.
Trong 50 viên bi được chia thành ba loại gồm: 16 viên bi có số chia hết cho 3; 17 viên bi có số chia cho 3 dư 1 và 17 viên bi còn lại có số chia cho 3 dư 2.
Để tìm số kết quả thuận lợi cho biến cố A, ta xét các trường hợp
● Trường hợp 1. 3 viên bi được chọn cùng một loại, có ![]() cách.
cách.
● Trường hợp 2. 3 viên bi được chọn có mỗi viên mỗi loại, có ![]() cách.
cách.
Suy ra số phần tử của biến cố A là ![]() .
.
Vậy xác suất cần tính 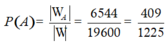
Chọn B.

HD: Xếp 10 học sinh thành 1 hàng ngang có:
![]()
Gọi A là biến cố: “Hàng ngang không có 2 bạn nữ nào đứng cạnh nhau”
Sắp xếp 5 bạn nam thành 1 hàng có: 5! cách sắp xếp, khi đó có 6 vị trị để xếp 5 bạn nữ xen kẽ để không có hai bạn nữ đứng cạnh nhau (6 vị trí bao gồm 2 vị trí đầu và cuối và 4 vị trí giữa 2 bạn nam)
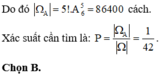

Cách 1:
n ( Ω ) = 10 !
Bước 1: Xếp 5 bạn nữ có: 5! Cách
Bước 2: Xếp 5 bạn nam vào xen giữa 4 khoảng trống của 5 bạn nữ và hai vị trí đầu hàng. Có hai trường hợp sau
+) TH1: Xếp 4 bạn nam vào 4 khoảng trống giữa 5 bạn nữ, bạn nam còn lại có hai lựa chọn:
Xếp vào hai vị trí đầu hàng. Trường hợp này có A 5 4 . 2 cách
+) TH2:
- Chọn một khoảng trống trong 4 khoảng trống giữa hai bạn nữ để xếp hai bạn nam có C 4 1 cách
- Chọn hai bạn nam trong 5 bạn nam để xếp vào vị trí đó có A 5 2 cách
- Ba khoảng trống còn lại xếp còn lại ba bạn nam còn lại có 3! Cách
Trường hợp này có C 4 1 . A 5 2 . 3 ! cách
Vậy có tất cả 5 ! ( A 5 4 . 2 + C 4 1 . A 5 2 . 3 ! ) cách
Vậy xác suất là: P = 5 ! ( A 5 4 . 2 + C 4 1 . A 5 2 . 3 ! ) 10 ! = 1 42
Cách 2:
n ( Ω ) = 10 !
- Xếp 5 bạn nam có 5! Cách
- Xếp 5 bạn nữ xen vào giữa 4 khoảng trống và 2 vị trí đầu hàng có A 6 5 cách
Vậy 5 ! . A 6 5 cách
Vậy P = 5 ! . A 6 5 10 ! = 1 42
Chọn đáp án B.

Có 5 viên bi lẻ
Số cách lấy 2 viên bất kì: \(C_{10}^2\)
2 viên bi có tích là lẻ khi cả 2 đều lẻ
Số cách lấy: \(C_5^2\)
Xác suất: \(P=\dfrac{C_5^2}{C_{10}^2}=\dfrac{2}{9}\)