Tất cả các giá trị x thỏa mãn bất phương trình log 3 x - 1 > 2 là
A. x > 10
B. x < 10
C. 0 < x < 10
D. x ≥ 10
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D.
Để f(x) ≤ 0 thì (x + 5)(3 - x) < 0
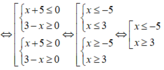
Vậy x ∈ (- ∞ ;-5] ∪ [3;+ ∞ ).

Ư(24)={ 1 ,2 ,3 ,4 ,6 ,8 ,12 ,24 }
Vậy A={ 12, 24 }
chúc bạn học tốt. Cho tick nha

Điều kiện 1 3 ≤ x ≤ 10
Bất phương trình đã cho tương đương với:
log 2 3 x + 1 + 6 - 1 ≥ log 2 7 - 10 - x ⇔ 3 x + 1 + 6 2 ≥ 7 - 10 - x ⇔ 3 x + 1 + 2 10 - x ≥ 8 ⇔ 3 x + 1 + 4 3 x + 1 10 - x + 4 10 - x ≥ 64 ⇔ 4 3 x + 1 10 - x ≥ x + 23 ⇔ 16 3 x + 1 10 - x ≥ x + 23 2 ⇔ 49 x 2 - 418 x + 369 ≤ 0 ⇔ 1 ≤ x ≤ 369 49 ≈ 7 , 5
Mà x ∈ ℤ nên x ∈ 1 ; 2 ; 3 ; 4 ; 5 ; 6 ; 7
Vậy có 7 giá trị nguyên của x
Đáp án D

Ta có bất phương trình thứ nhất:
\(2x+1< x+3\)
\(\Leftrightarrow2x-x< 3-1\)
\(\Leftrightarrow x\cdot\left(2-1\right)< 2\)
\(\Leftrightarrow x< 2\) (1)
Bất phương trình thứ hai:
\(5x\ge x-16\)
\(\Leftrightarrow5x-x\ge-16\)
\(\Leftrightarrow4x\ge-16\)
\(\Leftrightarrow x\ge-4\) (2)
Từ (1) và (2) ta có:
\(-4\le x< 2\)
2x+1<x+3 và 5x>=x-16
=>2x-x<3-1 và 5x-x>=-16
=>x<2 và x>=-4
=>-4<=x<2
Chọn đáp án A