Cho tam giác ABC có trung tuyến AM .Tỉ số diện tích giữa tam giác ABM và tam giác ACM là
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
30 tháng 1 2023
a: Sửa đề: BC=10cm và ΔABC vuông tại A
\(AC=\sqrt{10^2-6^2}=8\left(cm\right)\)
\(S_{ABC}=\dfrac{1}{2}\cdot6\cdot8=3\cdot8=24\left(cm^2\right)\)
b: Kẻ AH vuông góc BC
\(S_{ABM}=\dfrac{1}{2}\cdot AH\cdot BM\)
\(S_{ACM}=\dfrac{1}{2}\cdot AH\cdot CM\)
mà BM=CM
nên \(S_{ABM}=S_{ACM}\)
28 tháng 12 2018
Từ A kẻ đường thẳng AH vuông góc với BC ( H thuộc BC )
Ta có : \(S_{ABM}=\frac{1}{2}\cdot BM\cdot AH\)(1)
và \(S_{ACM}=\frac{1}{2}\cdot MC\cdot AH\)(2)
Mặt khác ta có AM là đường trung tuyến
=> \(BM=MC\)(3)
Từ (1), (2) và (3) ta có : \(S_{ABM}=S_{ACM}\left(đpcm\right)\)
10 tháng 3 2022
xét tam giác ABM và tam giác ACM ta có
AM=AM ( cạnh chung)
AB=AC( tam giác ABC cân tại A)
goc MAB = góc MAC ( AM là tia p.g góc BAC)
->tam giac ABM= tam giac ACM (c-g-c)
CM
28 tháng 2 2018
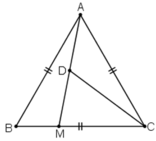
a) Do tam giác ABC là tam giác đều nên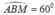 
.
Theo định lý côsin trong tam giác ABM ta có:
b) Theo định lý sin trong tam giác ABM ta có:
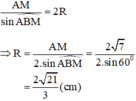
c) Ta có: BM + MC = BC nên MC = BC – BM = 6 - 2 = 4 cm.
Gọi D là trung điểm AM.
Áp dụng công thức độ dài đường trung tuyến trong tam giác ta có:
LT
14 tháng 1 2022
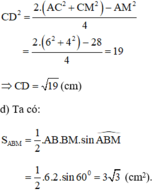
Đáp án:
a) Vì M là trung điểm của BC nên BM bằng CM.
Vì hình tam giác ABM và hình tam giác ACM có chung cạnh AM nên độ dài chiều cao của hình tam giác ABM và ABM bằng nhau.
→→Do có chung độ dài đáy và chiều cao bằng nhau nên diện tích hai hình tam giác bằng nhau.
Vậy diện tích hình tam giác ABM bằng diện tích hình tam giác ACM.
b) Vì BM bằng MC nên BM và MC bằng 1212 BC. Do đó diện tích hình tam giác ABM bằng 1/2 diện tích hình tam giác ABC.
Vậy diện tích hình tam giác ABM bằng 1/2 diện tích hình tam giác ABC.
Ht và tk
Trang cũng đăng câu này à?