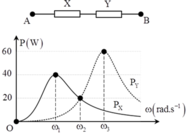
Lần lượt đặt điện áp u = U 2 cos ω t (U không đổi, ω thay đổi được) vào hai đầu đoạn mạch X và vào hai đầu đoạn mạch Y; với X và Y là các đoạn mạch R, L, C mắc nối tiếp. Trên hình vẽ, P X và P Y lần lượt biểu diễn quan hệ công suất tiêu thụ của X với ω và Y với ω. Sau đó, đặt điện áp u lên đoạn mạch AB gồm X và Y mắc nối tiếp. Biết cảm kháng của cuộn cảm thuần mắc nối tiếp (có cảm kháng Z L 1 và Z L 2 ) là Z L = Z L 1 + Z L 2 và dung kháng của hai tụ điện mắc nối tiếp (có dung kháng Z C 1 và Z C 2 ) là Z C = Z C 1 + Z C 2 . Khi ω = ω 2 , công suất tiêu thụ của đoạn mạch AB gần giá trị nào sau đây nhất?
A. 14 W
B. 10 W
C. 22 W
D. 24 W

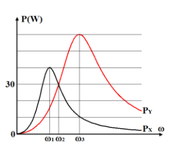
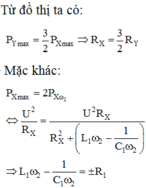


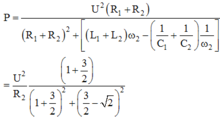

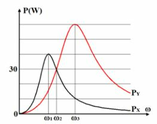
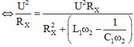
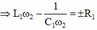
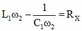
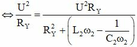
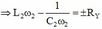
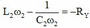
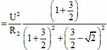
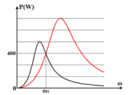
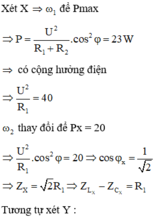
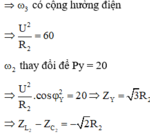

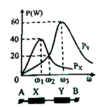
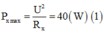
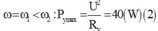
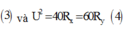

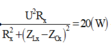
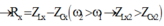
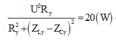
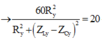
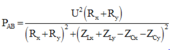
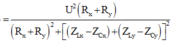

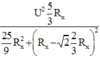
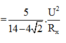
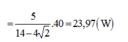
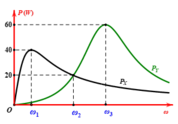

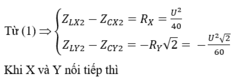
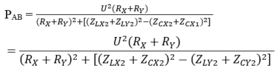
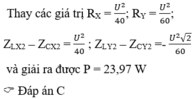
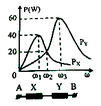
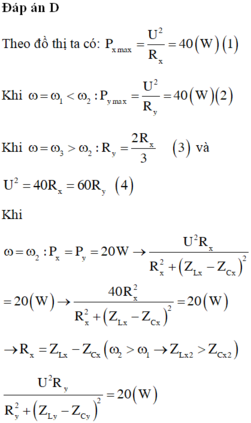
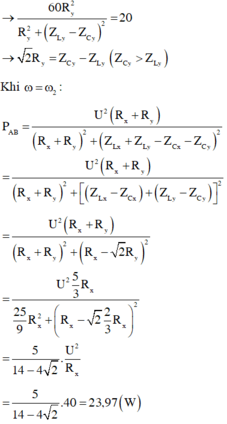
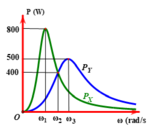


Từ đồ thị ta có: P Y max = 3 2 P X max ⇒ R X = 3 2 R Y
Mặc khác:
P X max = 2 P X ω 2 ⇔ U 2 R X = U 2 R X R X 2 + L 1 ω 2 − 1 C 1 ω 2 ⇒ L 1 ω 2 − 1 C 1 ω 2 = ± R 1
Ta chọn nghiệm L 1 ω 2 − 1 C 1 ω 2 = R X vì đồ thị P X tại giá trị ω 2 mạch đang có tính cảm kháng
Ta chọn nghiệm L 2 ω 2 − 1 C 2 ω 2 = − R Y vì đồ thị P Y tại giá trị ω 2 mạch đang có tính dung kháng
Công suất tiêu thụ của đoạn mạch AB tại ω 2 :
P = U 2 R 1 + R 2 R 1 + R 2 2 + L 1 + L 2 ω 2 − 1 C 1 + 1 C 2 1 ω 2 = U 2 R 2 1 + 3 2 1 + 3 2 2 + 3 2 − 2 2
Từ đó ta tính được P ω 2 = 23 , 97 W
Đáp án B