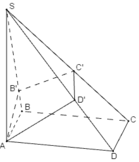
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA=2, SB=6, SC=9. Độ dài cạnh SD là
A. 7.
B. 11.
C. 5.
D. 8.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
18 tháng 2 2019
Đúng(0)
Những câu hỏi liên quan
CM
18 tháng 10 2017
Đáp án A
S A 2 + S C 2 = 2 h 2 + x 2 + y 2 + z 2 + t 2 = S B 2 + S D 2 .
Chú ý: Cách chứng minh cho trường hợp này cũng đúng khi H nằm ngoài miền của hình chữ nhật.
Lời bình: Có lẽ, việc xét hình chóp với SA vuông góc với mặt phẳng (ABC) dễ dàng cho ta nhận xét là S A 2 + S C 2 = S B 2 + S D 2 .
CM
15 tháng 4 2017
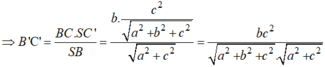
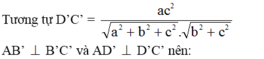S
∆
A
B
'
C
'
=
1
2
B
'
C
'
.
A
B
'
=
1
2
.
c
2
a
2
+
c
2
.
b
a
2
+
b
2
+
c
2
.
c
a
a
2
+
c
2
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 1
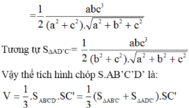
Trước hết ta chứng minh 1 bổ đề đơn giản về diện tích tam giác như sau (em tự vẽ hình)
Cho tam giác ABC, trên các cạnh AB và AC lần lượt lấy 2 điểm B' và C', khi đó ta có:
\(\dfrac{S_{AB'C'}}{S_{ABC}}=\dfrac{AB'.AC'}{AB.AC}\)
Chứng mình: từ C và C' lần lượt hạ CH và C'H' vuông góc AB, khi đó CH song song C'H' nên theo Talet:
\(\dfrac{C'H'}{CH}=\dfrac{AC'}{AC}\)
\(\Rightarrow\dfrac{S_{AB'C'}}{S_{ABC}}=\dfrac{\dfrac{1}{2}C'H'.AB'}{\dfrac{1}{2}CH.AB}=\dfrac{AC'.AB'}{AC.AB}\)
Quay lại bài, gọi O là tâm đáy
Trong mp (SAC), tại O' là giao điểm của SO và A'C'
Ba mặt phẳng (SAC), (SBD), \(\left(\alpha\right)\) cắt nhau theo 3 giao tuyến phân biệt là SO, A'C', B'D' nên 3 giao tuyến này song song hoặc đồng quy.
Mà SO và A'C' cắt nhau tại O' nên 3 đường thẳng nói trên đồng quy tại O'
Ta có:
\(S_{SA'C'}=S_{SA'O'}+S_{SC'O'}\Rightarrow\dfrac{S_{SA'C'}}{S_{SAC}}=\dfrac{S_{SA'O'}}{S_{SAC}}+\dfrac{S_{SC'O'}}{S_{SAC}}\)
\(\Rightarrow\dfrac{S_{SA'C'}}{S_{SAC}}=\dfrac{S_{SA'O'}}{2S_{SAO}}+\dfrac{S_{SC'O'}}{S_{SCO}}\Rightarrow\dfrac{SA'.SC'}{SA.SC}=\dfrac{SA'.SO'}{2SA.SO}+\dfrac{SC'.SO'}{2SC.SO}\)
\(\Leftrightarrow\dfrac{SA'.SC'}{SA.SC}=\dfrac{SO'}{2SO}\left(\dfrac{SA'}{SA}+\dfrac{SC'}{SC}\right)\)
\(\Leftrightarrow SA'.SC'=\dfrac{SO'}{2SO}\left(SC.SA'+SA.SC'\right)\)
\(\Leftrightarrow1=\dfrac{SO'}{2SO}\left(\dfrac{SC}{SC'}+\dfrac{SA}{SA'}\right)\)
\(\Leftrightarrow\dfrac{SA}{SA'}+\dfrac{SC}{SC'}=\dfrac{2SO}{SO'}\)
Hoàn toàn tương tự, ta cũng có \(\dfrac{SB}{SB'}+\dfrac{SD}{SD'}=\dfrac{2SO}{SO'}\)
\(\Rightarrow\dfrac{SA}{SA'}+\dfrac{SC}{SC'}-\left(\dfrac{SB}{SB'}+\dfrac{SD}{SD'}\right)=0\)
15 tháng 6 2023
a: BC vuông góc AB; BC vuông góc SA
=>BC vuông góc (SAB)
b: (BS;(BACD))=(BS;BA)=góc SBA
tan SBA=SA/AB=căn 5/2
=>góc SBA=48 độ
(SC;(ABCD))=(CS;CA)=góc SCA
tan SCA=SA/AC=1
=>góc SCA=45 độ
