Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án là D.
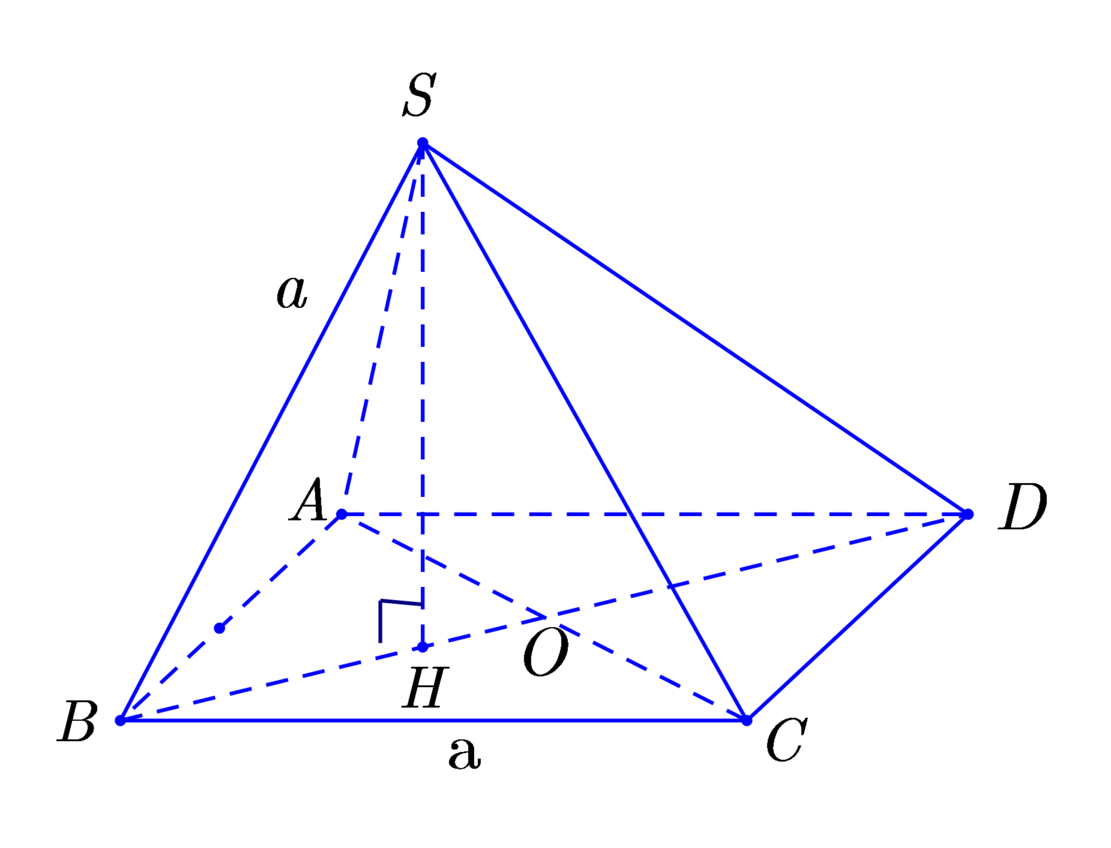
Khi SD thay đổi thi AC thay đổi. Đặt AC = x.
Gọi O = A C ∩ B D .
Vì S A = S B = S C nên chân đường cao SH trùng với tâm đường tròn ngoại tiếp tam giác ABC.
⇒ H ∈ B O
Ta có: O B = a 2 − x 2 2 = 4 a 2 − x 2 4 = 4 a 2 − x 2 2
S A B C = 1 2 O B . A C = 1 2 x . 4 a 2 − x 2 2 = x 4 a 2 − x 2 4
H B = R = a . a . x 4 S A B C = a 2 x 4. x 4 a 2 − x 2 4 = a 2 4 a 2 − x 2
S H = S B 2 − B H 2 = a 2 − a 4 4 a 2 − x 2 = a 3 a 2 − x 2 4 a 2 − x 2
S H = S B 2 − B H 2 = a 2 − a 4 4 a 2 − x 2 = a 3 a 2 − x 2 4 a 2 − x 2
= 1 3 a x . 3 a 2 − x 2 ≤ 1 3 a x 2 + 3 a 2 − x 2 2 = a 3 2

Đáp án là C
Hình chóp S.ABCD có đáy là hình chữ nhật, SA=SB=SC=SD có hai mặt đối xứng đó là mặt phẳng (SMN) và (SPQ) trong đó M, N, P, Q lần lượt là trung điểm của các cạnh đáy AB, CD, BC,AD

Đáp án B
Ta có: 2 B H 2 = a 3 2 ⇒ B H 2 = 3 a 2 2
S H = S B 2 − B H 2 = 2 a 2 − 3 a 2 2 = a 2
Thể tích khối chóp S.ABCD là:
V = 1 3 . S H . S A B C D = 1 3 . a 2 . a 3 2 = a 3 2

Chọn B.
Phương pháp:

Gọi I, J lần lượt là trung điểm của AB, CD.

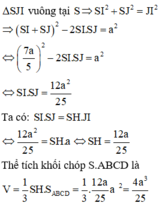

Đáp án A
Gọi E và F là trung điểm của AB và CD ta có: S E ⊥ A B ⇒ S E ⊥ C D ⇒ S E ⊥ giao tuyến của 2 mặt phẳng (SAB) và (SCD) vì giao tuyến này song song với AB.
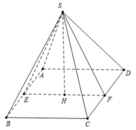
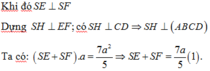
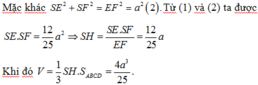

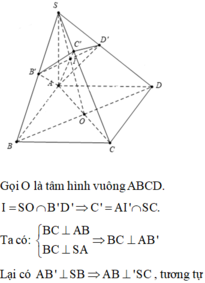


Đáp án A
S A 2 + S C 2 = 2 h 2 + x 2 + y 2 + z 2 + t 2 = S B 2 + S D 2 .
Chú ý: Cách chứng minh cho trường hợp này cũng đúng khi H nằm ngoài miền của hình chữ nhật.
Lời bình: Có lẽ, việc xét hình chóp với SA vuông góc với mặt phẳng (ABC) dễ dàng cho ta nhận xét là S A 2 + S C 2 = S B 2 + S D 2 .