Biết x,y là nghiệm của hệ sau C x y - C x y + 1 = 0 4 C x y - 5 C x y - 1 = 0 . Giá trị của x+y là
A. 26
B. 25
C. 27
D. 28
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
12 tháng 8 2018
Đúng(0)
Những câu hỏi liên quan
CM
25 tháng 11 2017
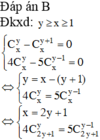
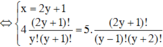
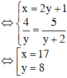
Chú ý. Đối với những hệ phương trình có hệ số thập phân như thế này ta nên nhân với 10 để có hệ phương trình hệ số nguyên:
Thay vào ta thấy phương án A sai, còn phương án B đúng. Vậy đáp án là B.
Đáp án: B
18 tháng 6 2020
\(\left\{{}\begin{matrix}x+2y=2\\2x-2y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x=3\\x+2y=2\end{matrix}\right.\Leftrightarrow}\left\{{}\begin{matrix}x=1\\y=\frac{1}{2}\end{matrix}\right.\)
HQ
Hà Quang Minh
Giáo viên
24 tháng 9 2023
a)
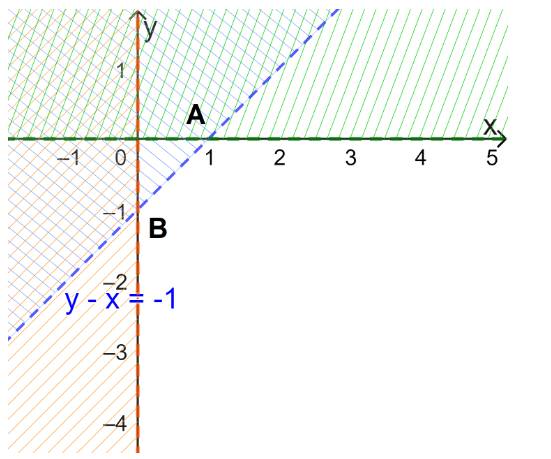
Xác định miền nghiệm của BPT \(y - x < - 1\)
+ Vẽ đường thẳng d: \(y-x= - 1\) đi qua A(1;0) và B(0;-1)
+ Vì \(0-0= 0 > - 1\) nên tọa độ điểm O(0;0) không thỏa mãn BPT \(y - x < - 1\)
Do đó, miền nghiệm của BPT \(y - x < - 1\) là nửa mặt phẳng bờ d không chứa gốc tọa độ O.
Miền nghiệm của BPT \(x > 0\) là nửa mặt phẳng bên phải Oy (không kể trục Oy).
Miền nghiệm của BPT \(y < 0\) là nửa mặt phẳng dưới Ox (không kể trục Ox).
Khi đó miền nghiệm của hệ bất phương trình đã cho là miền không gạch (Không kể đoạn thẳng AB và các trục tọa độ).
b)
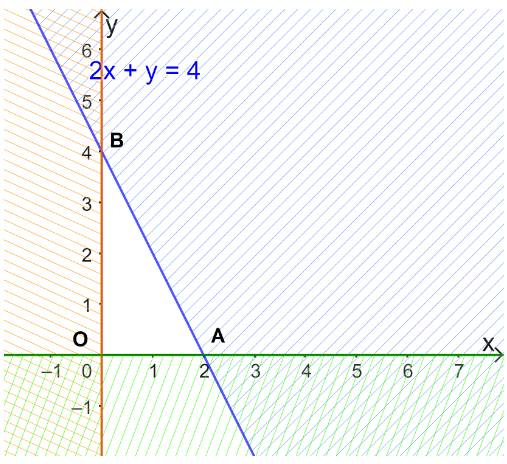
Miền nghiệm của BPT \(x \ge 0\) là nửa mặt phẳng bờ Oy chứa điểm (1;0) (kể cả trục Oy).
Miền nghiệm của BPT \(y \ge 0\) là nửa mặt phẳng bờ Ox chứa điểm (0;1) (kể cả trục Ox).
Xác định miền nghiệm của bất phương trình \(2x + y \le 4\)
+ Vẽ đường thẳng d: \(2x + y = 4\) đi qua A(2;0) và B(0;4)
+ Vì \(2.0 + 0 = 0 < 4\) nên tọa độ điểm O(0;0) thỏa mãn BPT \(2x + y \le 4\)
Do đó, miền nghiệm của bất phương trình \(2x + y \le 4\) là nửa mặt phẳng bờ d chứa gốc tọa độ O.
Vậy miền nghiệm của hệ bất phương trình đã cho là miền tam giác OAB (kể cả các đoạn thẳng OA, OB, AB).
c)
Miền nghiệm của bất phương trình \(x \ge 0\) là nửa mặt phẳng bên phải Oy (kể cả trục Oy).
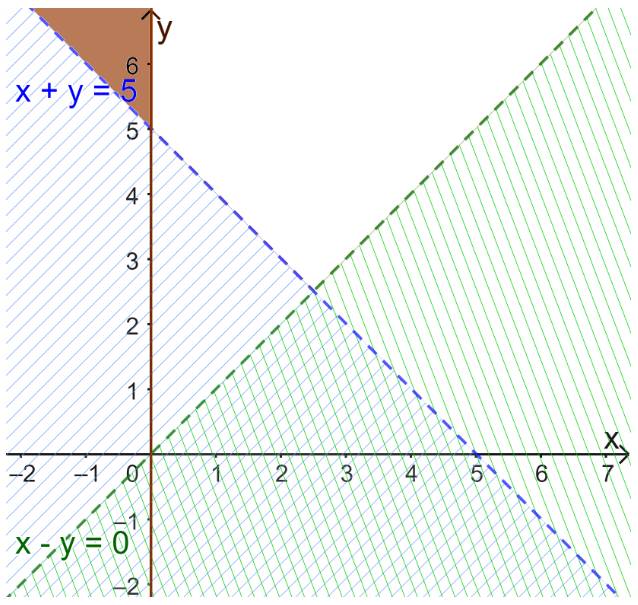
Xác định miền nghiệm của bất phương trình \(x + y > 5\)
+ Vẽ đường thẳng d: \(x + y = 5\)
+ Vì \(0 + 0 = 0 < 5\) nên tọa độ điểm O(0;0) không thỏa mãn bất phương trình \(x + y > 5\).
Do đó, miền nghiệm của BPT \(x + y > 5\) là nửa mặt phẳng bờ d không chứa gốc tọa độ O.
Xác định miền nghiệm của bất phương trình \(x - y < 0\)
+ Vẽ đường thẳng d: \(x - y = 0\)
+ Vì \(1 - 0 = 1 > 0\) nên tọa độ điểm (1;0) không thỏa mãn bất phương trình \(x - y < 0\)
Do đó, miền nghiệm của bất phương trình \(x - y < 0\) là nửa mặt phẳng bờ d’ không chứa điểm (1;0).
Vậy miền nghiệm của hệ bất phương trình đã cho là miền màu trắng (không kể d và d’)
